题目内容
下列函数中，既是偶函数又在区间（0，+∞）上递增的函数为（ ）
| A、y=x3 |
| B、y=|log2x| |
| C、y=-x2 |
| D、y=|x| |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：根据偶函数的定义，偶函数定义域的特点，二次函数的单调性即可判断每个选项的正误．
解答：
解：y=x3是奇函数；
函数y=|log2x|的定义域（0，+∞）不关于原点对称，所以是非奇非偶函数；
y=-x2在（0，+∞）上单调递减；
函数y=|x|=
是偶函数，且在区间（0，+∞）上递增；
∴D正确．
故选D．
函数y=|log2x|的定义域（0，+∞）不关于原点对称，所以是非奇非偶函数；
y=-x2在（0，+∞）上单调递减；
函数y=|x|=
|
∴D正确．
故选D．
点评：考查偶函数、奇函数的定义，偶函数定义域的特点，二次函数的单调性，一次函数的单调性．
练习册系列答案
相关题目
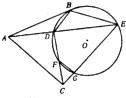如图，AB是⊙O的切线，B为切点，ADE是⊙O的割线，C是⊙O外一点，且AB=AC，连接BD，BE，CD，CE，CD交⊙O于F，CE交⊙O于G．
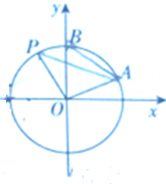如图，一个半径为R的圆上一点A（