题目内容
19.将函数$f(x)=2sin({x+\frac{π}{6}})+1$的图象向右平移$\frac{π}{3}$个单位,再把所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得函数y=g(x)的图象,则g(x)图象的一个对称中心为( )| A. | $({\frac{π}{6},0})$ | B. | $({\frac{π}{12},0})$ | C. | $({\frac{π}{6},1})$ | D. | $({\frac{π}{12},1})$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用正弦函数的图象的对称性,求得g(x)图象的一个对称中心.
解答 解:将函数$f(x)=2sin({x+\frac{π}{6}})+1$的图象向右平移$\frac{π}{3}$个单位,可得y=2sin(x-$\frac{π}{3}$+$\frac{π}{6}$)-1=2sin(x-$\frac{π}{6}$)+1的图象;
再把所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),可得y=g(x)=2sin(2x-$\frac{π}{6}$)+1的图象.
令2x-$\frac{π}{6}$=kπ,k∈Z,求得x=$\frac{kπ}{2}$+$\frac{π}{12}$,令k=0,可得g(x)图象的一个对称中心为($\frac{π}{12}$,1),
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
10.已知实数 x,y满足$\left\{\begin{array}{l}x+y≥a\\ x-y≤a\\ y≤a\end{array}\right.({a>0})$,若z=x2+y2的最小值为 2,则 a的值为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
7.若函数$f(x)=sin2ωx+2\sqrt{3}{cos^2}ωx-\sqrt{3}(ω>0)$在$[\frac{π}{2},π]$上单调递减,则ω的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{4}]$ | B. | $[\frac{1}{6},\frac{7}{12}]$ | C. | $[\frac{1}{4},\frac{1}{2}]$ | D. | $[0,\frac{1}{2}]$ |
8.已知a=21.3,b=40.7,c=ln6,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
9.若方程|lnx|=a有两个不等的实根x1和x2,则x1+x2的取值范围是( )
| A. | (1,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (0,1) |
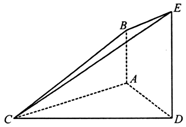 如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB.