题目内容
若(
-
)9的展开式中x3项的系数为
.
(1)求a的值;
(2)求证:a15-1能被2a-1整除.
| a |
| x |
|
| 9 |
| 4 |
(1)求a的值;
(2)求证:a15-1能被2a-1整除.
考点:二项式系数的性质,二项式定理的应用,整除的基本性质
专题:二项式定理
分析:(1)直接利用二项式定理的展开式求出常数项,得到关系式即可求a的值;
(2)通过(1)化简a15-1,利用二项式定理,证明表达式能被2a-1整除.
(2)通过(1)化简a15-1,利用二项式定理,证明表达式能被2a-1整除.
解答:
(本小题满分16分)
解:(1)通项Tr+1=C9r(
)9-r•(-
)r=C9ra9-r(-
)rx
-9,
令
-9=0 得r=8,
∴C98a9-8(-
)8=
a=
,
∴a=4.
(2)当a=4时,2a-1=7,
a15-1=230-1
=(7+1)10-1
=C100710+C10179+…+C1010-1
=C100710+C10179+…+C1097,
因为每一项都是7的倍数,所以能被7整除.得证.
解:(1)通项Tr+1=C9r(
| a |
| x |
|
| 1 |
| 2 |
| 3r |
| 2 |
令
| 3r |
| 2 |
∴C98a9-8(-
| 1 |
| 2 |
| 9 |
| 16 |
| 9 |
| 4 |
∴a=4.
(2)当a=4时,2a-1=7,
a15-1=230-1
=(7+1)10-1
=C100710+C10179+…+C1010-1
=C100710+C10179+…+C1097,
因为每一项都是7的倍数,所以能被7整除.得证.
点评:本题考查二项式定理的应用,考查基本知识的应用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
平行线3x-4y-3=0和6x-8y+5=0之间的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
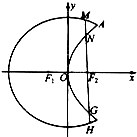 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆