题目内容
已知数列{an}，a1=2，an=an-12，求数列{an}的通项公式．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由已知结合数列递推式求出a2，a3，a4，猜测数列{an}的通项公式，由归纳法证明得答案．
解答：
解：由a1=2，an=an-12，得
a2=a12=4=22，
a3=a22=16=24，
a4=a32=28，
…
∴an=22n-1．
证明：当n=1时，a1=2=220，结论成立；
假设n=k时结论成立，即ak=22k-1，
当n=k+1时，ak+1=ak2=(22k-1)2=22•2k-1=22k+1-1．
综上，n=k+1时结论成立．
a2=a12=4=22，
a3=a22=16=24，
a4=a32=28，
…
∴an=22n-1．
证明：当n=1时，a1=2=220，结论成立；
假设n=k时结论成立，即ak=22k-1，
当n=k+1时，ak+1=ak2=(22k-1)2=22•2k-1=22k+1-1．
综上，n=k+1时结论成立．
点评：本题考查了数列递推式，考查了归纳法证明与自然数有关的命题，是中档题．
练习册系列答案
相关题目
在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC=AD=CD=DE=2，AB=1．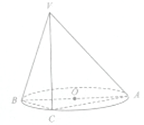
如图，AB是⊙0的直径，点C是⊙0上的点，过点C的直线VC垂直于⊙0所在平面，且AC=