题目内容
求直线
(t为参数)被曲线ρ=
cos(θ-
)所截的弦长,将方程
,ρ=
cos(θ+
)分别化为普通方程.
|
| 2 |
| π |
| 4 |
|
| 2 |
| π |
| 4 |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:由直线
(t为参数)消去参数t可得3x+4y+1=0,由曲线ρ=
cos(θ+
)展开化为x2+y2=x-y,
配方为(x-
)2+(y+
)2=
,可得圆心C,半径r.利用点到直线的距离公式得出圆心到直线的距离d.再利用弦长|AB|=2
即可得出.
|
| 2 |
| π |
| 4 |
配方为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| r2-d2 |
解答:
解:由直线
(t为参数)消去参数t可得3x+4y+1=0,
由曲线ρ=
cos(θ+
)可得ρ2=
ρ(
cosθ-
sinθ),化为x2+y2=x-y,
配方为(x-
)2+(y+
)2=
,可得圆心C(
,-
),半径r=
.
圆心到直线的距离d=
=
.
∴弦长|AB|=2
=
.
|
由曲线ρ=
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
配方为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
圆心到直线的距离d=
|3×
| ||||
|
| 1 |
| 10 |
∴弦长|AB|=2
| r2-d2 |
| 7 |
| 5 |
点评:本题考查了参数方程极坐标方程化为普通方程、圆的标准方程、点到直线的距离公式、弦长公式,考查了计算能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
设P={x|x≤8},a=
,则下列关系中,正确的是( )
| 61 |
| A、a⊆P |
| B、a∉P |
| C、{a}∈P |
| D、{a}是P的真子集 |
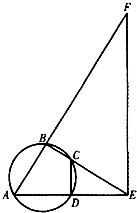 如图,A、B、C、D四点共圆,BC和AD的延长线交于点E,点F在AB的延长线上.
如图,A、B、C、D四点共圆,BC和AD的延长线交于点E,点F在AB的延长线上.