题目内容
已知向量
=(-1,2),又点A(8,0),B(n,t),C(k,t).
(Ⅰ)若
⊥
,且|
|=
|
|(O为坐标原点),求向量
;
(Ⅱ)若向量
与向量
共线,且tk取最大值时,求
•
.
| a |
(Ⅰ)若
| AB |
| a |
| AB |
| 5 |
| OA |
| OB |
(Ⅱ)若向量
| AC |
| a |
| OA |
| OC |
考点:平面向量数量积的运算,平行向量与共线向量
专题:平面向量及应用
分析:本题(1)利用向量垂直的坐标表示及向量模的坐标表示,列出关于n,t的方程组,求出方程组的解即可;(2)向量
向与量
共线,得出t,k的关系式,根据tk的最大值,求出k,t的值,得到
•
的值.
| AC |
| a |
| OA |
| OC |
解答:
解:(Ⅰ)∵点A(8,0),B(n,t),
∴
=(n-8,t),
=(8,0).
∵向量
=(-1,2),
⊥
,
∴8-n+2t=0,
∴n=2t+8.①
又∵|
|=
|
|,
∴(n-8)2+t2=5×64.②
∴t=±8.
当t=8时,n=24;当t=-8时,n=-8.
∴
=(24,8)或
=(-8,-8)
(2)∵点A(8,0),C(k,t),
∴
=(k-8,t).
∵向量
=(-1,2),向量
与向量
共线,
∴t=16-2k.
∴tk=(16-2k)k=-2k2+16k=-2(k-4)2+32≤32,
∴当tk最大时,k=4,t=8,
此时,
•
=8k+t=40.
∴
| AB |
| OA |
∵向量
| a |
| AB |
| a |
∴8-n+2t=0,
∴n=2t+8.①
又∵|
| AB |
| 5 |
| OA |
∴(n-8)2+t2=5×64.②
∴t=±8.
当t=8时,n=24;当t=-8时,n=-8.
∴
| OB |
| OB |
(2)∵点A(8,0),C(k,t),
∴
| AC |
∵向量
| a |
| AC |
| a |
∴t=16-2k.
∴tk=(16-2k)k=-2k2+16k=-2(k-4)2+32≤32,
∴当tk最大时,k=4,t=8,
此时,
| OA |
| OC |
点评:本题考查向量共线、垂直的坐标表示、向量的模的计算,函数最值求解,分类讨论、计算等思想方法和能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
下列事件为随机事件的是( )
| A、抛一个硬币,落地后正面朝上或反面朝下 |
| B、百分制考试中,小强考试成绩为105分 |
| C、相邻两边分别为a,b的长方形面积为ab |
| D、信州区下周一下雪 |
 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.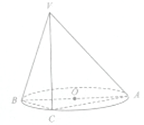 如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=
如图,AB是⊙0的直径,点C是⊙0上的点,过点C的直线VC垂直于⊙0所在平面,且AC=