题目内容
已知数列{an}中,a1=-
,且2an+1+anan+1+1=0(n∈N*).
(1)求a2,a3,a4;
(2)猜想数列通项公式an,并用数学归纳法证明.
| 1 |
| 2 |
(1)求a2,a3,a4;
(2)猜想数列通项公式an,并用数学归纳法证明.
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)根据a1=-
,且2an+1+anan+1+1=0,利用递推公式,求出aa2,a3,a4.
(2)总结出规律求出an,然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
| 1 |
| 2 |
(2)总结出规律求出an,然后利用归纳法进行证明,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答:
(1)解:由a1=-
,且2an+1+anan+1+1=0得a2=-
,a3=-
,a4=-
(2)an=-
.
证明:①n=1时,结论成立,
②假设n=k时,结论成立,即ak=-
,
则n=k+1时,由2ak+1+akak+1+1=0,
得:ak+1=-
=
,即n=k+1时等式也成立,
由①②可知an=-
.
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
(2)an=-
| n |
| n+1 |
证明:①n=1时,结论成立,
②假设n=k时,结论成立,即ak=-
| k |
| k+1 |
则n=k+1时,由2ak+1+akak+1+1=0,
得:ak+1=-
| k+1 |
| k+2 |
| k+1 |
| (k+1)+1 |
由①②可知an=-
| n |
| n+1 |
点评:此题主要考查归纳法的证明,归纳法一般三个步骤:(1)验证n=1成立;(2)假设n=k成立;(3)利用已知条件证明n=k+1也成立,从而求证,这是数列的通项一种常用求解的方法.

练习册系列答案
相关题目
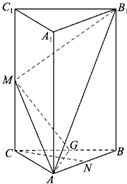 如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=