题目内容
13.已知log23=a,log35=b,则lg6=( )| A. | $\frac{1}{1+ab}$ | B. | $\frac{a}{1+ab}$ | C. | $\frac{b}{1+ab}$ | D. | $\frac{a+1}{1+ab}$ |
分析 由已知结合对数的换底公式求得lg2及lg3的值,再由对数的运算性质求得lg6.
解答 解:∵log23=a,log35=b,
∴$\frac{lg3}{lg2}=a$,$\frac{lg5}{lg3}=\frac{1-lg2}{lg3}=b$,
解得:$lg2=\frac{1}{1+ab},lg3=\frac{a}{1+ab}$,
∴lg6=$lg2+lg3=\frac{1}{1+ab}+\frac{a}{1+ab}=\frac{1+a}{1+ab}$.
故选:D.
点评 本题考查对数的运算性质,考查了换底公式的应用,是基础题.

练习册系列答案
相关题目
1.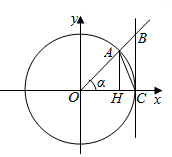 如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )
如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )
 如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )
如图所示,在单位圆O中,∠AOH=α(0<α<$\frac{π}{2}$),若△AOH的面积记为S1,△BOC的面积记为S2,△AOC的面积为S3,扇形AOC的面积记为S4,则( )| A. | S1=$\frac{1}{2}$sinα | B. | S2=$\frac{1}{2}$tanα | C. | S3=α | D. | S4=$\frac{1}{2}$cosα |
18.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)在区间(0,π)上存在唯一一个x0∈(0,π),使得f(x0)=1,则ω的取值范围为( )
| A. | ($\frac{1}{2}$,$\frac{11}{6}$] | B. | [$\frac{1}{2}$,$\frac{11}{6}$) | C. | ($\frac{1}{3}$,$\frac{13}{6}$] | D. | [$\frac{1}{3}$,$\frac{13}{6}$) |
2.已知数列{an}为等差数列,且公差d>0,数列{bn}为等比数列,若a1=b1>0,a4=b4,则( )
| A. | a7>b7 | B. | a7=b7 | ||
| C. | a7<b7 | D. | a7与b7大小无法确定 |
14.$\frac{3+i}{1-i}$的虚部为( )
| A. | 2 | B. | -2 | C. | -2i | D. | 2i |