题目内容
9. 如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2
如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2(1)证明:平面PAD⊥平面ABFE;
(2)若正四棱锥P-ABCD的体积是三棱锥P-ABF体积的4倍,求正四棱锥P-ABCD的高.
分析 (1)证明AD⊥平面ABFE,即可证明平面PAD⊥平面ABFE.
(2)连结BD与AC交于点O,连结PO,推导出P到平面ABEF的距离等于O到平面ABEF的距离,从而P到平面ABF的距离为d=1,由此能求出正四棱锥P-ABCD的高.
解答 证明:(1)直三棱柱ADE-BCF中,∵AB⊥平面ADE,
∴AB⊥AD,又AD⊥AF,
∴AD⊥平面ABFE,AD?平面PAD,
∴平面PAD⊥平面ABFE….(6分)
解:(2)连结BD与AC交于点O,连结PO,
∵正四棱锥P-ABCD,∴PO⊥平面ABCD,
又∵直三棱柱ADE-BCF,∴AB⊥AE,且有AD⊥平面ABEF,
∴AD⊥AE,
∴AE⊥平面ABCD,则PO∥AE,
∵AE?平面ABEF,∴PO∥平面ABEF,
则P到平面ABEF的距离等于O到平面ABEF的距离,
又∵O为BD中点,∴O到平面ABEF的距离为$\frac{1}{2}AD$=1,
∴P到平面ABF的距离为d=1,
∴${V}_{P-ABF}=\frac{1}{3}{S}_{△ABF}•d$=$\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$,
设正四棱锥P-ABCD的高为h,
∵正四棱锥P-ABCD的体积是三棱锥P-ABF体积的4倍,
∴${V}_{P-ABCD}=\frac{1}{3}{S}_{△ABCD}•h=\frac{1}{3}×2×2h$=4VP-ABF=$\frac{8}{3}$,
解得h=2,
∴正四棱锥P-ABCD的高为2.
点评 本题主要考查空间面面垂直的判断以及正四棱棱的高的求解,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
19.已知a,b∈R,则命题“若a+b=1,则a2+b2≥$\frac{1}{2}$”的逆否命题是( )
| A. | 若a+b≠1,则a2+b2<$\frac{1}{2}$ | B. | 若a+b=1,则a2+b2<$\frac{1}{2}$ | ||
| C. | 若a2+b2<$\frac{1}{2}$,则a+b≠1 | D. | 若a2+b2≥$\frac{1}{2}$,则a+b=1 |
14.如图,正三棱柱(底面为正三角形,侧棱垂直底面)的正视图面积a2,则侧视图的面积为( )
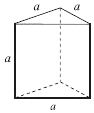

| A. | a2 | B. | $\frac{{\sqrt{3}}}{2}{a^2}$ | C. | $\sqrt{3}{a^2}$ | D. | $\frac{{\sqrt{3}}}{4}{a^2}$ |
18.若直线l经过A(2,1),B(1,-m2)(m∈R)两点,则直线l的倾斜角α的取值范围是( )
| A. | 0≤α≤$\frac{π}{4}$ | B. | $\frac{π}{2}$<α<π | C. | $\frac{π}{4}$≤α<$\frac{π}{2}$ | D. | $\frac{π}{2}$<α≤$\frac{3π}{4}$ |
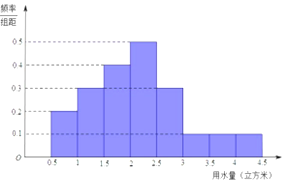 某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:
某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图: