题目内容
4.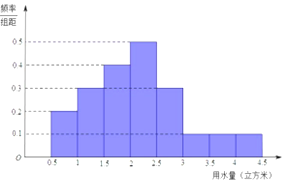 某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:
某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:(1)如果w 为整数,那么根据此次调查,为使40%以上居民在该月的用水价格为2元/立方米,w 至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=2 时,估计该市居民该月的人均水费.
分析 (1)1)由频率分布直方图得:用水量在[0.5,1)的频率为0.1,用水量在[1,1.5)的频率为0.15,用水量在[1.5,2]的频率是0.2,从而求出w的最小值;
(2)当w=2时,利用频率分布直方图能求出该市居民的人均水费.
解答 解:(1)我市居民用水量在区间[0.5,1],(1,1.5],(1.5,2]内的频率依次是:
0.1、0.15、0.2、
∴该月用水量不超过2立方米的居民占45%,
而用水量不超过1立方米的居民占10%,
∴w至少定为2;
(2)根据题意,列出居民该月用水费用的数据分组与频率分布表:
| 组号 | 用水量区间 | 人均费用 | 频率 |
| 1 | [0.5,1] | 2 | 0.1 |
| 2 | (1,1.5] | 3 | 0.15 |
| 3 | (1.5,2] | 4 | 0.2 |
| 4 | (2,2.5] | 6 | 0.25 |
| 5 | (2.5,3] | 8 | 0.15 |
| 6 | (3,3.5] | 10 | 0.05 |
| 7 | (3,5,4] | 12 | 0.05 |
| 8 | (4,4.5] | 16 | 0.05 |
2×0.1+3×0.15+4×0.2+6×0.25+8×0.15+10×0.05+12×0.05+16×0,05=6.05,
故w=2时,该市居民该月的人均水费约是6.05元.
点评 本题考查频率分布直方图的应用,考查当w=2时,该市居民该月的人均水费的估计的求法,是中档题,解题时要认真审题,注意频率分布直方图的合理运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
16.命题“?x∈R,x2-2x+5≤0”的否定为( )
| A. | ?x∈R,x2-2x+5≥0 | B. | ?x∉R,x2-2x+5≤0 | C. | ?x∈R,x2-2x+5>0 | D. | ?x∉R,x2-2x+5>0 |
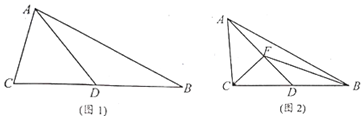
 如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2
如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2