题目内容
1.a,b,c三个数成等比数列,其中a=7+4$\sqrt{3}$,c=7-4$\sqrt{3}$,则b=±1.分析 由a,b,c三个数成等比数列,得到b=±$\sqrt{ac}$,由此能求出实数b.
解答 解:∵a,b,c三个数成等比数列,其中a=7+4$\sqrt{3}$,c=7-4$\sqrt{3}$,
∴b=±$\sqrt{ac}$=$\sqrt{(7+4\sqrt{3})(7-4\sqrt{3})}$=±1.
故答案为:±1.
点评 本题考查等比数列中第二项的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
11. 如图,已知长方体ABCD-A1B1C1D1的体积为6,∠C1BC的正切值为$\frac{1}{3}$,当AB+AD+AA1的值最小时,长方体ABCD-A1B1C1D1外接球的表面积( )
如图,已知长方体ABCD-A1B1C1D1的体积为6,∠C1BC的正切值为$\frac{1}{3}$,当AB+AD+AA1的值最小时,长方体ABCD-A1B1C1D1外接球的表面积( )
 如图,已知长方体ABCD-A1B1C1D1的体积为6,∠C1BC的正切值为$\frac{1}{3}$,当AB+AD+AA1的值最小时,长方体ABCD-A1B1C1D1外接球的表面积( )
如图,已知长方体ABCD-A1B1C1D1的体积为6,∠C1BC的正切值为$\frac{1}{3}$,当AB+AD+AA1的值最小时,长方体ABCD-A1B1C1D1外接球的表面积( )| A. | 10π | B. | 12π | C. | 14π | D. | 16π |
16.命题“?x∈R,x2-2x+5≤0”的否定为( )
| A. | ?x∈R,x2-2x+5≥0 | B. | ?x∉R,x2-2x+5≤0 | C. | ?x∈R,x2-2x+5>0 | D. | ?x∉R,x2-2x+5>0 |
10.圆心在直线$y=\frac{1}{3}x$上的圆C与y轴的正半轴相切,圆C截x轴所得的弦长为$4\sqrt{2}$,则圆C的标准方程为( )
| A. | (x-3)2+(y-1)2=9 | B. | (x+3)2+(y+1)2=9 | C. | ${({x-4})^2}+{({y-\frac{4}{3}})^2}=16$ | D. | (x-6)2+(y-2)2=9 |
11.已知抛物线y2=2px(p>0)上的点A到焦点F距离为4,若在y轴上存点B(0,2)使得$\overrightarrow{BA}$$•\overrightarrow{BF}$=0,则该抛物线的方程为( )
| A. | y2=8x | B. | y2=6x | C. | y2=4x | D. | y2=2x |
 如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2
如图所示,该几何体是一个由直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2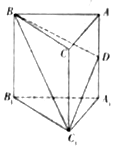 如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点
如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=8,D是AA1的中点