题目内容
9.设集合U=R,A={x|(x+1)(x-2)<0,则∁UA=( )| A. | (∞,-1)∪(2,+∞) | B. | [-1,2] | C. | (∞,-1]∪[2,+∞) | D. | (-1,2) |
分析 根据题意,解不等式(x+1)(x-2)<0可得集合A,又由补集的定义计算可得∁UA,即可得答案.
解答 解:根据题意,(x+1)(x-2)<0⇒-1<x<2,则集合A={x|(x+1)(x-2)<0}=(-1,2),
又由U=R,
则∁UA=(∞,-1]∪[2,+∞);
故选:C.
点评 本题考查集合补集的运算,关键是理解集合补集的定义.

练习册系列答案
相关题目
19.在区间[0,4]上随机产生两个均匀随机数分别赋给a,b,则|a-b|≤1的概率为( )
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{23}{32}$ |
20.若$\overrightarrow{a}$=(6,m),$\overrightarrow{b}$=(-1,3),且$\overrightarrow{a}⊥\overrightarrow{b}$,则m=( )
| A. | .2 | B. | .-2 | C. | .3 | D. | 6 |
4.二项式(x+1)n(n∈N+)的展开式中x2与x4系数相同,则n=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 7 |
13.圆的极坐标方程为ρ=2(cosθ+sinθ),则该圆的圆心极坐标是( )
| A. | $({1,\frac{π}{4}})$ | B. | $({\frac{1}{2},\frac{π}{4}})$ | C. | $(\sqrt{2},\frac{π}{4})$ | D. | $({2,\frac{π}{4}})$ |
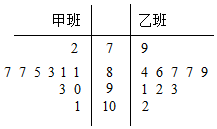 某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下: