题目内容
20.若$\overrightarrow{a}$=(6,m),$\overrightarrow{b}$=(-1,3),且$\overrightarrow{a}⊥\overrightarrow{b}$,则m=( )| A. | .2 | B. | .-2 | C. | .3 | D. | 6 |
分析 利用向量垂直与数量积的关系即可得出.
解答 解:∵$\overrightarrow{a}⊥\overrightarrow{b}$,∴$\overrightarrow{a}•\overrightarrow{b}$=-6+3m=0,则m=2.
故选:A.
点评 本题考查了向量垂直与数量积的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.已知$\overrightarrow a=(2,1)$,$\overrightarrow b=(3,-2)$,则 $\overrightarrow a•\overrightarrow b$的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
8.下列函数中是偶函数的有( )
| A. | y=x2 | B. | y=x | C. | y=x3 | D. | y=2x |
12.($\sqrt{x}+\frac{1}{2\sqrt{x}}$)8的展开式中常数项为( )
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
9.设集合U=R,A={x|(x+1)(x-2)<0,则∁UA=( )
| A. | (∞,-1)∪(2,+∞) | B. | [-1,2] | C. | (∞,-1]∪[2,+∞) | D. | (-1,2) |
4.将函数$y=sin(x+\frac{π}{6})$的图象向左平移π个单位,则平移后的函数图象( )
| A. | 关于直线$x=\frac{π}{3}$对称 | B. | 关于直线$x=\frac{π}{6}$对称 | ||
| C. | 关于点$(\frac{π}{3},0)$对称 | D. | 关于点$(\frac{π}{6},0)$对称 |
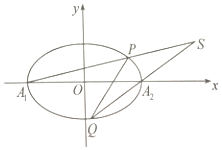 已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).
已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).