题目内容
1.已知抛物线的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y={t}^{2}}\end{array}\right.$(t为参数),焦点为F,直线x+2y-12=0与该抛物线交于A,B两点,则△ABF的面积为25.分析 求出抛物线的普通方程,直线x+2y-12=0与该抛物线联立,可得x2+2x-24=0,x=4或-6,即可求出△ABF的面积.
解答 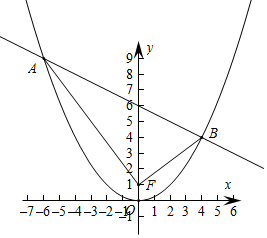 解:抛物线的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y={t}^{2}}\end{array}\right.$(t为参数),普通方程为x2=4y,焦点为F(0,1),
解:抛物线的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y={t}^{2}}\end{array}\right.$(t为参数),普通方程为x2=4y,焦点为F(0,1),
直线x+2y-12=0与该抛物线联立,可得x2+2x-24=0,∴x=4或-6,
直线x+2y-12=0,令x=0,可得y=6
∴△ABF的面积为$\frac{1}{2}×(6-1)×(4+6)$=25,
故答案为25.
点评 本题考查抛物线的参数方程,考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
11.已知$\overrightarrow a=(2,1)$,$\overrightarrow b=(3,-2)$,则 $\overrightarrow a•\overrightarrow b$的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
12.($\sqrt{x}+\frac{1}{2\sqrt{x}}$)8的展开式中常数项为( )
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
9.设集合U=R,A={x|(x+1)(x-2)<0,则∁UA=( )
| A. | (∞,-1)∪(2,+∞) | B. | [-1,2] | C. | (∞,-1]∪[2,+∞) | D. | (-1,2) |
16.一组数据分别为12,16,20,23,20,15,23,则这组数据的中位数是( )
| A. | 19 | B. | 20 | C. | 21.5 | D. | 23 |
4.将函数$y=sin(x+\frac{π}{6})$的图象向左平移π个单位,则平移后的函数图象( )
| A. | 关于直线$x=\frac{π}{3}$对称 | B. | 关于直线$x=\frac{π}{6}$对称 | ||
| C. | 关于点$(\frac{π}{3},0)$对称 | D. | 关于点$(\frac{π}{6},0)$对称 |
5.两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2017项为a2017,则a2017-5=( )


| A. | 2023×2017 | B. | 2023×2016 | C. | 1008×2023 | D. | 2017×1008 |
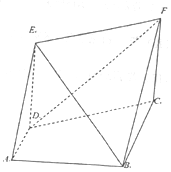 如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.
如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.