题目内容
17．sin347°cos148°+sin77°cos58°=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |
分析 由条件利用诱导公式、两角和差的余弦公式求得所给式子的值．
解答 解：sin347°cos148°+sin77°cos58°=-sin13°•（-cos32°）+cos13°sin32°
=sin（13°+32°）=sin45°=$\frac{\sqrt{2}}{2}$，
故选：B．
点评 本题主要考查诱导公式、两角和差的余弦公式的应用，属于基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
7．对于函数f（x），若存在x0∈Z，满足|f（x0）|≤$\frac{1}{4}$，则称x0为函数f（x）的一个“近零点”．已知函数f（x）=ax2+bx+c（a＞0）有四个不同的“近零点”，则a的最大值为（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
5．
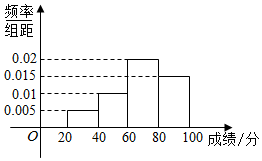某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）
某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）| A． | 50 | B． | 54 | C． | 60 | D． | 64 |
12．圆Г的圆周上六个点将圆周等分，经过这6个点中任意两点做圆的弦，在所做的这些弦中任意取出两条，则这两条弦有公共点的概率为（ ）
| A． | $\frac{5}{7}$ | B． | $\frac{4}{7}$ | C． | $\frac{1}{3}$ | D． | $\frac{4}{15}$ |
6．已知圆锥的母线长为20cm，则当其体积最大时，其侧面积为（ ）
| A． | $\frac{800\sqrt{6}π}{3}$cm2 | B． | $\frac{400\sqrt{6}π}{3}$cm2 | C． | $\frac{100\sqrt{6}π}{3}$cm2 | D． | $\frac{200\sqrt{6}π}{3}$cm2 |