题目内容
8.已知曲线C上每一点到点F(2,0)的距离与到直线x=-2的距离相等(Ⅰ)求曲线C的方程
(Ⅱ)直线过点p(a,0)a>0,且与曲线C有两个焦点A,B,O为坐标原点,求△AOB面积的最小值.
分析 (I)依题意知,动点M到定点F(2,0)的距离等于M到直线x=-2的距离,由抛物线的定义求出曲线C的方程;
(II)设直线l的方程为x=my+a,代入抛物线方程,利用韦达定理,即可得出结论.
解答 解:(Ⅰ)∵曲线C上的每一点到定点F(2,0)的距离与到定直线l:x=-2的距离相等,
∴轨迹为焦点在x轴上,以F(2,0)为焦点的抛物线
标准方程为:y2=8x
(Ⅱ)设直线l的方程为x=my+a,代入抛物线方程,可得:y2-8my-8a=0
设A(x1,y1),B(x2,y2),则y1+y2=8m,y1y2=-8a,
∴△AOB的面积=$\frac{1}{2}$•a•|y1-y2|=$\frac{1}{2}$•aπ$\sqrt{64{m}^{2}+32a}$≥2a$\sqrt{2a}$,
即m=0,△AOB的面积最小值为2a$\sqrt{2a}$.
点评 本题主要考查了轨迹方程,考查直线与圆锥曲线的综合问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
16.已知直线x-ay=4在y轴上的截距是2,则a等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
13.在△ABC中,已知三条边上的高线长分别为$\frac{1}{3}$,$\frac{1}{5}$,$\frac{1}{7}$,则△ABC的最大内角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
20.有一名同学家开了小卖部,他为了研究气温对某种饮料销售的影响,记录了2015年7月至12月每月15号的下午14时的气温和当天卖出的饮料杯数,得到如下资料:
改同学确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选中的2组数据进行检验.
(1)求选取2组数据恰好是相邻两个月的概率;
(2)若选中的是8月与12月的两组数据,根据剩下的4组数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据误差不超过3杯,则认为得到的线性回归方程是理想的,请问(2)所得到的线性回归方程是否理想.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n})({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
| 日期 | 7月15日 | 8月15日 | 9月15日 | 10月15日 | 11月15日 | 12月15日 |
| 摄氏温度x(℃) | 36 | 35 | 30 | 24 | 18 | 8 |
| 饮料杯数y | 27 | 29 | 24 | 18 | 15 | 5 |
(1)求选取2组数据恰好是相邻两个月的概率;
(2)若选中的是8月与12月的两组数据,根据剩下的4组数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据误差不超过3杯,则认为得到的线性回归方程是理想的,请问(2)所得到的线性回归方程是否理想.
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线y=bx+a的斜率和截距的最小二乘估计分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n})({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
17.sin347°cos148°+sin77°cos58°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
18.函数f(x)=lg(4-x2)的定义域为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,2) | C. | [-2,2] | D. | (-∞,-2)∪[2,+∞) |
 如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.
如图,设四棱柱ABCD-A1B1C1D1的底面为菱形,A1C与底面垂直.过点C作平面与四棱柱的侧棱垂直,且分别交A1A于点E,交BB1于点F,交DD1于点G.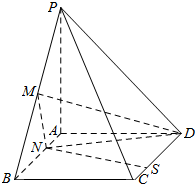 已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.
已知四棱锥P-ABCD中,面ABCD为矩形,PA⊥面ABCD,$PA=AD=\frac{1}{2}AB$,M为PB的中点,N、S分别为AB、CD上的点,且$AN=CS=\frac{1}{4}AB$.