题目内容
2.已知f(x)是定义在R上且周期为4的函数,在区间[-2,2]上,$f(x)=\left\{\begin{array}{l}mx+2,-2≤x<0\\ \frac{nx-2}{x+1},0≤x≤2\end{array}\right.$,其中m,n∈R,若f(1)=f(3),则$\frac{1}{4}\int_{-1}^3{(mx+n})dx$=8.分析 由函数的周期性可得f(-2)=f(2),f(1)=f(-1),可得m和n的方程组,解方程组求解定积分可得.
解答 解:∵f(x)是定义在R上且周期为4的函数,在区间[-2,2]上
有$f(x)=\left\{\begin{array}{l}mx+2,-2≤x<0\\ \frac{nx-2}{x+1},0≤x≤2\end{array}\right.$,且f(1)=f(3),
∴f(-2)=f(2),f(1)=f(3)=f(-1),
∴-2m+2=$\frac{2n-2}{3}$,$\frac{n-2}{2}$=-m+2,
联立解得m=-2,n=10,
∴$\frac{1}{4}\int_{-1}^3{(mx+n})dx$=$\frac{1}{4}$•($\frac{1}{2}$mx2+nx)${|}_{-1}^{3}$=m+n=8
故答案为:8
点评 本题考查定积分的求解,涉及分段函数以及函数的周期性,属中档题.

练习册系列答案
相关题目
14.如表提供了某新生婴儿成长过程中时间x(月)与相应的体重y(公斤)的几组对照数据.
(1)如y与x具有较好的线性关系,请根据表中提供的数据,求出线性回归方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)由此推测当婴儿生长到五个月时的体重为多少?
参考公式:$\stackrel{∧}{y}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$;$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=27.5.
| x | 0 | 1 | 2 | 3 |
| y | 3 | 3.5 | 4.5 | 5 |
(2)由此推测当婴儿生长到五个月时的体重为多少?
参考公式:$\stackrel{∧}{y}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$;$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=27.5.
11.已知函数f(x)=x3-12x+8在区间[-3,3]上的最大值与最小值分别为M、m,则$\frac{M}{m}$等于( )
| A. | -24 | B. | -17 | C. | -3 | D. | 3 |
12.过点A(0,2)与抛物线C:y2=4x恰有一个交点的直线有( )条.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
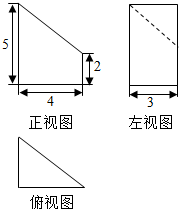
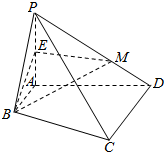 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.