题目内容
10.已知点F是抛物线y2=2px(p>0)的焦点,P(2,y0)是抛物线上一点,若|PF|=3,则p=2.分析 根据抛物线上的点到焦点和准线的距离相等,可得p值.
解答 解:∵点F是抛物线y2=2px(p>0)的焦点,P(2,y0)是抛物线上一点,|PF|=3,
∴2+$\frac{p}{2}$=3,
解得:p=2,
故答案为:2.
点评 本题考查的知识点是抛物线的简单性质,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.圆x2+y2-6x+4y+12=0与圆(x-7)2+(y-1)2=36的位置关系是( )
| A. | 外切 | B. | 相交 | C. | 内切 | D. | 外离 |
5.为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为t1和t2,已知两人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是( )
| A. | t1和t2有交点(s,t) | B. | t1与t2相交,但交点不一定是(s,t) | ||
| C. | t1与t2必定平行 | D. | t1与t2必定重合 |
19.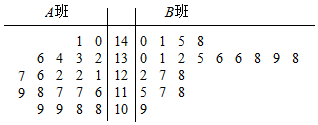 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
市数学会规定:140分以上(含140分)为市级一等奖,135分以上(含135分)为市级二等奖,100分以上(含100分)为市级三等奖.
(1)由茎叶图判断A班和B班的平均分$\overline{{x}_{A}}$,$\overline{{x}_{B}}$的大小(只需写出结论);
(2)按照规则:获得市一等奖、二等奖的同学才能获得省里组织的“全国数学联赛”复赛资格,我们称这些同学为“种子选手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为称为‘种子’选手”与班级有关?
(3)在获市级一等奖的同学中选出3人,求至少含有1名A班同学的概率.
下面临界值表仅供参考:
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:
为备战“全国高中数学联赛”,我市某高中拟成立两个“数学竞赛班”,经过学校预选,选出40名学生,编成A,B两个班,分别由两位教师担任教练进行培训;经过两个月的培训,参加了市里组织的数学竞赛初赛(只有经过初赛,取得相应名次,才能取得参加省统一组织的“全国高中数学联赛”复赛资格),这40名学生的初赛成绩的茎叶图如图:市数学会规定:140分以上(含140分)为市级一等奖,135分以上(含135分)为市级二等奖,100分以上(含100分)为市级三等奖.
(1)由茎叶图判断A班和B班的平均分$\overline{{x}_{A}}$,$\overline{{x}_{B}}$的大小(只需写出结论);
(2)按照规则:获得市一等奖、二等奖的同学才能获得省里组织的“全国数学联赛”复赛资格,我们称这些同学为“种子选手”,请填写下面的2×2列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为称为‘种子’选手”与班级有关?
| A班 | B班 | 合计 | |
| 种子选手 | |||
| 非种子选手 | |||
| 合计 |
下面临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知等差数列{an}中,前n项和为Sn,a1>0,a1007+a1008=0,则当Sn取最大值时,n=( )
| A. | 1007 | B. | 1008 | C. | 2014 | D. | 2015 |
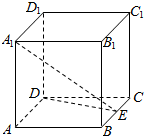 如图,在正方体ABCD-A1B1C1D1中,AB=2,点E是BC的中点.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E是BC的中点.