题目内容
13.某几何体的三视图如图所示,则该几何体的体积为24.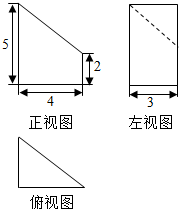
分析 由已知中的三视图可得该几何体是一个三棱柱截去一个三棱锥所得的组合体,分别计算出棱柱和棱锥的体积,可得答案
解答 解:由已知中的三视图可得该几何体是一个三棱柱截去一个三棱锥所得的组合体,
其中棱柱的体积为:$\frac{1}{2}$×4×3×5=30,
截去的棱锥的体积为:$\frac{1}{3}$×$\frac{1}{2}$×4×3×(5-2)=6,
故该几何体的体积V=30-6=24;
故答案为:24.
点评 本题考查的知识点是由三视图求体积和表面积,根据已知中的三视图,判断出几何体的形状是解答的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
12.已知等比数列{an}的各项均为正数,且a1+a2=$\frac{4}{9}$,a3+a4+a5+a6=40.则$\frac{{a}_{7}+{a}_{8}+{a}_{9}}{9}$的值为117.
1.圆x2+y2-6x+4y+12=0与圆(x-7)2+(y-1)2=36的位置关系是( )
| A. | 外切 | B. | 相交 | C. | 内切 | D. | 外离 |
8.已知圆心为点C(4,-3),且过原点,则圆的方程为( )
| A. | (x+4)2+(y-3)2=25 | B. | (x+4)2+(y-3)2=5 | C. | (x-4)2+(y+3)2=25 | D. | (x-4)2+(y+3)2=5 |
5.为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为t1和t2,已知两人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是( )
| A. | t1和t2有交点(s,t) | B. | t1与t2相交,但交点不一定是(s,t) | ||
| C. | t1与t2必定平行 | D. | t1与t2必定重合 |
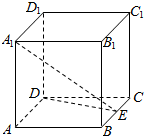 如图,在正方体ABCD-A1B1C1D1中,AB=2,点E是BC的中点.
如图,在正方体ABCD-A1B1C1D1中,AB=2,点E是BC的中点. 如图,正方形ABCD的边长为3,M为DC的中点,若N为正方形内任意一点(含边界),则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为$\frac{27}{2}$.
如图,正方形ABCD的边长为3,M为DC的中点,若N为正方形内任意一点(含边界),则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为$\frac{27}{2}$.