题目内容
已知数列{an}中,an+1=Sn-n+3,n∈N*,a1=2.
(Ⅰ)求证:当n≥2,n∈N*时,{an-1}是等比数列;
(Ⅱ)求{an}的通项公式;
(Ⅲ)利用错位相减法求出Tn,即可证明不等式
≤Tn<
(n∈N*).
(Ⅰ)求证:当n≥2,n∈N*时,{an-1}是等比数列;
(Ⅱ)求{an}的通项公式;
(Ⅲ)利用错位相减法求出Tn,即可证明不等式
| 1 |
| 3 |
| 4 |
| 3 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)根据等比数列的定义即可证明:当n≥2,n∈N*时,{an-1}是等比数列;
(Ⅱ)利用{an-1}是等比数列,即可求{an}的通项公式;
(Ⅲ)设bn=
(n∈N*)的前n项和为Tn,求证:
≤Tn<
(n∈N*).
(Ⅱ)利用{an-1}是等比数列,即可求{an}的通项公式;
(Ⅲ)设bn=
| n |
| Sn-n+2 |
| 1 |
| 3 |
| 4 |
| 3 |
解答:
解:(Ⅰ)∵
,
∴an+1-an=an-1⇒an+1-1=2(an-1),
∴{an-1}从第二项起为公比等于2的等比数列.
(Ⅱ)∵{an-1}从第二项起为公比等于2的等比数列.
∴a2=S1-1+3=4,a1=2a2-1≠2(a1-1),
∴an=
.
(Ⅲ)由(Ⅱ)知Sn=an+1+n-3=3×2n-1+n-2⇒bn=
,
则Tn=
(
+
+???+
),
Tn=
(
+
+???+
),
两式相减得
Tn=
(1+
+
+???+
-
)=
Tn=
?(
-
)=
?(2-
),
即Tn=
-
,
∵bn>0∴Tn≥T1=
,
∴
≤Tn<
.
|
∴an+1-an=an-1⇒an+1-1=2(an-1),
∴{an-1}从第二项起为公比等于2的等比数列.
(Ⅱ)∵{an-1}从第二项起为公比等于2的等比数列.
∴a2=S1-1+3=4,a1=2a2-1≠2(a1-1),
∴an=
|
(Ⅲ)由(Ⅱ)知Sn=an+1+n-3=3×2n-1+n-2⇒bn=
| n |
| 3×2n-1 |
则Tn=
| 1 |
| 3 |
| 1 |
| 20 |
| 2 |
| 21 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 21 |
| 2 |
| 22 |
| n |
| 2n |
两式相减得
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 3 |
1-(
| ||
1-
|
| n |
| 2n |
| 1 |
| 3 |
| n+2 |
| 2n |
即Tn=
| 4 |
| 3 |
| 2n+4 |
| 3•2n |
∵bn>0∴Tn≥T1=
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查等比数列的应用,以及考查数列求通项、错位相减法求和,考查学生的计算能力.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )
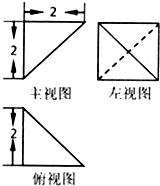

| A、8π | B、12π |
| C、16π | D、48π |
已知向量
的模为2
,
=(1,-2),条件p:向量
的坐标为(4,2),条件q:
⊥
,则p是q的( )
| a |
| 5 |
| b |
| a |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |




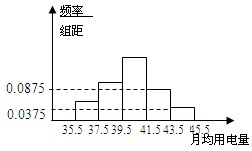 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3. 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.