题目内容
已知二项式（1-2i）6则展开式的第四项为 ．
考点：二项式系数的性质
专题：数系的扩充和复数,二项式定理
分析：根据二项式展开式的通项公式，求出展开式的第四项即可．
解答：
解：∵二项式（1-2i）6展开式的第四项为
T3+1=
•16-3•（-2i）3
=20×1×（-8）×（-i）
=160i．
∴展开式的第四项为160i．
故答案为：160i．
T3+1=
| C | 3 6 |
=20×1×（-8）×（-i）
=160i．
∴展开式的第四项为160i．
故答案为：160i．
点评：不同考查了二项式展开式的通项公式的应用问题，也考查了复数的应用问题，是基础题目．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设集合M={x|x=
，k∈Z}，N={x|x=
+
，k∈Z}，则M、N之间的关系为（ ）
| kπ |
| 2 |
| + |
. |
| π |
| 4 |
| kπ |
| 4 |
| π |
| 2 |
| A、M?N | B、M?N |
| C、M=N | D、M∩N=∅ |
如图，以正方形ABCD的边长为直径作半圆，重叠部分为花瓣（如图阴影部分），现在向该正方形区域内随机地投掷一飞镖，求飞镖落在花瓣内的概率．如图为函数f（x）=t+logax的图象（a，t均为实常数），则下列结论正确的是 （ ）
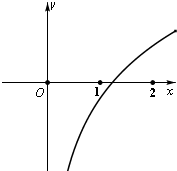
| A、0＜a＜1，t＜0 |
| B、0＜a＜1，t＞0 |
| C、a＞1，t＜0 |
| D、a＞1，t＞0 |
已知某人打靶时，每次击中目标的概率是0.8，现采用随机模拟的方法估计此人打靶三次恰有两次击中目标的概率：先由计算器算出0到4之间取整数值的随机数，指定0，1，2，3表示击中，4表示不击中；再以每三个随机数为一组，代表3次打靶的结果．经随机模拟产生了20组随机数：
据此估计，此人打靶三次恰有两次击中目标的额概率是（ ）
据此估计，此人打靶三次恰有两次击中目标的额概率是（ ）
| A、0.348 | B、0.35 |
| C、0.3 | D、0.6 |
已知|
|=
，
=（1-λ）
+λ
，若
•
=0，
•
=1，则λ=（ ）
| a |
| 2 |
| c |
| a |
| b |
| a |
| b |
| a |
| c |
| A、1 | ||
B、-
| ||
C、
| ||
| D、-1 |
如图所示，程序执行后的输出结果为（ ）
| A、-1 | B、0 | C、1 | D、2 |
若甲、乙、丙三人随机地站成一排，则甲、乙两人相邻而站的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|