题目内容

7．下面是关于函数y=ax2+bx+c，a≠0，x∈M，M为非空集合，关于最值的论述：
（1）当a＞0时，函数一定有最小值为$\frac{{4ac-{b^2}}}{4a}$；
（2）y是否有最大值和最小值，关键取决于x的范围，有可能y既有最大值，也有最小值，其值不一定是$\frac{{4ac-{b^2}}}{4a}$；
（3）求y的最大值或最小值时，利用公式：$x=-\frac{b}{2a}$求出对称轴，再画草图，根据x的范围截取图象，最后根据图象确定取最大值或最小值时对应的x值，然后通过代入求得最值．
以上结论中正确的个数有（　　）
A．0B．1C．2D．3

分析 根据二次函数的性质判断即可．

解答 解：（1）当a＞0时，x∈M，M为非空集合，若M是开区间，则函数没有最小值，（1）错误；
（2）y是否有最大值和最小值，关键取决于x的范围，有可能y既有最大值，也有最小值，其值不一定是$\frac{{4ac-{b^2}}}{4a}$，故（2）正确；
（3）求y的最大值或最小值时，利用公式：$x=-\frac{b}{2a}$求出对称轴，再画草图，根据x的范围截取图象，最后根据图象确定取最大值或最小值时对应的x值，然后通过代入求得最值，故（3）正确；
以上结论中正确的个数有2个，
故选：C．

点评 本题考察了二次函数的性质，是一道基础题．

练习册系列答案
相关题目
18．已知sin（x+$\frac{π}{3}$）=$\frac{1}{3}$，则cosx+cos（$\frac{π}{3}$-x）的值为（　　）
A．-$\frac{\sqrt{3}}{3}$B．$\frac{\sqrt{3}}{3}$C．-$\frac{1}{3}$D．$\frac{1}{3}$
18．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线l与直线l′：x+$\sqrt{3}$y=0垂直，垂足为O，过C的右焦点F分别作l，l′的垂线，垂足分别为N，P，若四边形ONFP的面积为$\sqrt{3}$，则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$．
15．已知函数$f（x）=\frac{{{x^4}+k{x^2}+1}}{{{x^4}+{x^2}+1}}\;（k∈R）$，若对任意三个实数a、b、c，均存在一个以f（a）、f（b）、f（c）为三边之长的三角形，则k的取值范围是（　　）
A．-2＜k＜4B．$-\frac{1}{2}＜k＜4$C．-2＜k≤1D．$-\frac{1}{2}＜k≤1$
2．已知等差数列{an}前四项中第二项为606，前四项和S4为3883，则该数列第4项为（　　）
A．3074B．2065C．2024D．2016
12．已知定义在（-∞，0）∪（0，+∞）上的奇函数f（x）满足f（2）=0，且在（-∞，0）上是增函数；又定义行列式|$\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}$|=a1a4-a2a3； 函数g（θ）=|$\begin{array}{l}{sinθ}&{3-cosθ}\\{m}&{sinθ}\end{array}$|（其中0≤θ≤$\frac{π}{2}$）．
（1）证明：函数f（x）在（0，+∞）上也是增函数；
（2）若函数g（θ）的最大值为4，求m的值；
（3）若记集合M={m|任意的0≤θ≤$\frac{π}{2}$，g（θ）＞0}，N={m|任意的0≤θ≤$\frac{π}{2}$，f[g（θ）]＜0}，求M∩N．
19．已知直线y=kx+1与双曲线3x2-y2=3的右支相交于不同的两点，则k的取值范围是$（-2，-\sqrt{3}）$．
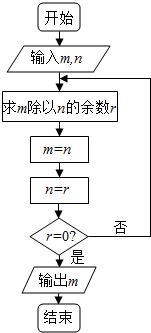16．如图的程序图的算法思路中是一种古老而有效的算法--辗转相除法，执行改程序框图，若输入的m，n的值分别为30，42，则输出的m=（　　）
A．0B．2C．3D．6
17．已知定义在实数集R上的偶函数f（x）和奇函数g（x）满足f（x）+g（x）=2x+1．
（1）求f（x）与g（x）的解析式；
（2）若定义在实数集R上的以2为最小正周期的周期函数φ（x），当-1≤x≤1时，φ（x）=f（x），试求φ（x）在闭区间[2015，2016]上的表达式，并证明φ（x）在闭区间[2015，2016]上单调递减；
（3）设h（x）=x2+2mx+m2-m+1（其中m为常数），若h（g（x））≥m2-m-1对于x∈[1，2]恒成立，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网