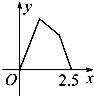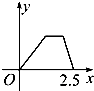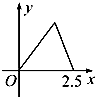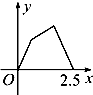题目内容
已知函数y=x2+
(a∈R)在x=1处的切线与直线2x-y+1=0平行,且此切线也是圆x2+y2+mx-(3m+1)y=0的切线,则m= .
| a |
| x |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:求出函数的导数,求得切线的斜率,由两直线平行的条件可得a,求得切点,求出切线方程,求出圆的圆心和半径,应用直线与圆相切则d=r,由点到直线的距离公式,列出方程,解出m即可.
解答:
解:∵函数y=x2+
(a∈R)在x=1处的切线与直线2x-y+1=0平行,
∴f′(1)=2,
由于f′(x)=2x-
,
即f′(1)=2-a=2,解得a=0,
函数y=x2,
则切点为(1,1),切线方程为:y-1=2(x-1),
即2x-y-1=0,
由于圆x2+y2+mx-(3m+1)y=0的圆心为(-
,
),半径为
,
由直线与圆相切得,
=
,
化简,解得m=±
.
故答案为:±
.
| a |
| x |
∴f′(1)=2,
由于f′(x)=2x-
| a |
| x2 |
即f′(1)=2-a=2,解得a=0,
函数y=x2,
则切点为(1,1),切线方程为:y-1=2(x-1),
即2x-y-1=0,
由于圆x2+y2+mx-(3m+1)y=0的圆心为(-
| m |
| 2 |
| 3m+1 |
| 2 |
| ||
| 2 |
由直线与圆相切得,
|2×(-
| ||||
|
| ||
| 2 |
化简,解得m=±
| 2 |
| 5 |
故答案为:±
| 2 |
| 5 |
点评:本题考查导数的应用:求切线方程,考查直线与圆相切的条件,考查运算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=log2
是( )
| 1+x |
| 1-x |
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
如图,阴影部分表示的集合是( )


| A、B∩[∁U (A∪C)] |
| B、(A∪B)∪(B∪C) |
| C、(A∪C)∩(∁UB) |
| D、[∁U (A∩C)]∪B |
 在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.
在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.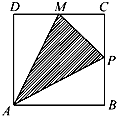 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )