题目内容
下列函数中,最小正周期为π的偶函数为( )
A、y=sin(x+
| ||||
B、y=
| ||||
| C、y=2tan2x | ||||
| D、y=sinxcosx |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的图像与性质
分析:A:y=
sin(2x+
)=
cos2x,可求得其最小正周期并能判断其奇偶性;
B:y=
=cotx,可判断其正误;
C:易求y=tan2x的最小正周期为
,可排除C;
D:y=
sin2x为奇函数,从而可排除D.
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
B:y=
| 1+cos2x |
| sin2x |
C:易求y=tan2x的最小正周期为
| π |
| 2 |
D:y=
| 1 |
| 2 |
解答:
解:A:∵y=f(x)=
sin(2x+
)=
cos2x,∴其最小正周期T=π,
又f(-x)=
cos(-2x)=
cos2x=f(x),
∴y=sin(x+
)cos(x+
)为偶函数,故A正确;
B:∵y=
=cotx为奇函数,故可排除B;
C:∵y=tan2x的最小正周期为T=
,故可排除C;
D:∵y=
sin2x为奇函数,故可排除D.
故选:A.
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
又f(-x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴y=sin(x+
| π |
| 4 |
| π |
| 4 |
B:∵y=
| 1+cos2x |
| sin2x |
C:∵y=tan2x的最小正周期为T=
| π |
| 2 |
D:∵y=
| 1 |
| 2 |
故选:A.
点评:本题考查三角函数中的恒等变换,着重考查三角函数的周期性与奇偶性,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知一个几何体的三视图如图所示,则该几何体的表面积为( )


| A、10π+96 |
| B、9π+96 |
| C、8π+96 |
| D、9π+80 |
点(1,1,1)关于z轴的对称点为( )
| A、(-1,-1,1) |
| B、(1,-1,-1) |
| C、(-1,1,-1) |
| D、(-1,-1,-1) |
将八进制数131(8)化为二进制数为( )
| A、1011001(2) |
| B、1001101(2) |
| C、1000011(2) |
| D、1100001(2) |
若用秦九韶算法求多项式f(x)=4x5-x2+2当x=3时的值,则需要做乘法运算和加减法运算的次数分别为( )
| A、4,2 | B、5,3 |
| C、5,2 | D、6,2 |
如图是一个正三角形场地,如果在每边上放2盆花共需要3盆花;如果在每边上放3盆花共需要6盆花,如果在每边上放n(n>1)盆花,那么共需要花( )盆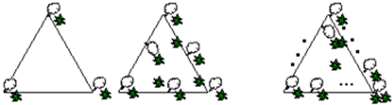

| A、3n | B、3n-1 |
| C、3n-2 | D、3n-3 |
 如图,正三棱柱ABC-A1B1C1的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为
如图,正三棱柱ABC-A1B1C1的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为