题目内容
在极坐标系中,已知圆C经过点P(
,
),圆心为直线ρsin(θ-
)=-
与极轴的交点,则圆C的极坐标方程是 .
| 2 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把直线的极坐标方程化为直角坐标方程,求出圆心和半径,可得圆的标准方程,再化为极坐标方程.
解答:
解:点P(
,
)的直角坐标为(1,1),
直线ρsin(θ-
)=-
的直角坐标方程为
y-
x=-
,即
x-y-
=0,
此直线和极轴的交点为(1,0),即所求圆的圆心C,故半径为CP=1,
故所求的圆的方程为 (x-1)2+y2=1,化为极坐标方程为ρ=2cosθ,
故答案为:ρ=2cosθ.
| 2 |
| π |
| 4 |
直线ρsin(θ-
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
此直线和极轴的交点为(1,0),即所求圆的圆心C,故半径为CP=1,
故所求的圆的方程为 (x-1)2+y2=1,化为极坐标方程为ρ=2cosθ,
故答案为:ρ=2cosθ.
点评:本题主要考查极坐标方程与直角坐标方程的互化,求圆的标准方程,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列{an}的前n项和为Sn,若
=a1
+a20
,且A、B、C三点共线(该直线不过点O),则S20=( )
| OB |
| OA |
| OC |
| A、10 | B、11 | C、20 | D、21 |

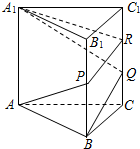 已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=
已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=