题目内容
10.函数f(x)=-x3+ax2-x-1在R上不单调,则实数a的取值范围是( )| A. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | B. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
分析 求出函数的导数,由题意得函数的导数在R上至少有一个零点,主要不能有两个相等的零点,即可求出实数a的取值范围.
解答 解:∵f(x)=-x3+ax2-x-1,
∴f′(x)=-3x2+2ax-1,
∵若函数f(x)=-x3+ax2-x-1在R上不是单调函数
∴f′(x)=-3x2+2ax-1=0有两个不等的根,
即△=4a2-12>0,
解得a<-$\sqrt{3}$,或a>$\sqrt{3}$,
故选:B.
点评 本题考查了利用导数研究三次多项式函数的单调性,从而求参数a的取值范围,属于基础题,解题时应该注意导函数等于0的等根的情形,以免出现只一个零点的误解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
20.直线2x+(1-a)y+2=0与直线ax-3y-2=0平行,则a=( )
| A. | 2或3 | B. | -2或3 | C. | -2 | D. | 3 |
1.已知函数f(x)=$\left\{\begin{array}{l}{(2a-1)x+4a,x<1}\\{1+lo{g}_{a}x,x≥1}\end{array}\right.$是R上的减函数,则实数a的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
5.在△ABC中,a,b,c分别是内角A,B,C所对的边,已知a=4,B=60°,C=75°,则b=( )
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\frac{11}{3}$ |
2.设U={1,2,3,4,5},A={1,2,5},B={2,3,4},则B∩∁UA=( )
| A. | ∅ | B. | {2} | C. | {3,4} | D. | {1,3,4,5} |
7.已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf'(x)+f(x)≤0,对任意的0<a<b,则必有( )
| A. | af(b)≤bf(a) | B. | bf(a)≤af(b) | C. | af(a)≤f(b) | D. | bf(b)≤f(a) |
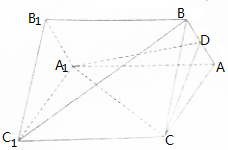 如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.