题目内容
11.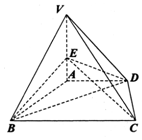 如图,四棱锥V-ABCD的底面是直角梯形,VA⊥面ABCD,AD∥BC,AD⊥CD,VA=AD=CD=$\frac{1}{2}$BC=a,点E是棱VA上不同于A,V的点.
如图,四棱锥V-ABCD的底面是直角梯形,VA⊥面ABCD,AD∥BC,AD⊥CD,VA=AD=CD=$\frac{1}{2}$BC=a,点E是棱VA上不同于A,V的点.(1)求证:无论点E在VA如何移动都有AB⊥CE;
(2)设二面角A-BE-D的大小为α,直线VC与平面ABCD所成的角为β,试确定点E的位置使$tanαtanβ=\frac{{\sqrt{2}}}{2}$.
分析 (1)连接AC,推导出AB⊥AC,AB⊥AV,由此能证明AB⊥CE.
(2)取BC中点F,以点A为坐标原点,AF,AD,AV所在的直线为x,y,z轴,建立空间直角坐标系A-xyz,利用向量法能求出点E为VA的中点.
解答 证明:(1)连接AC,在直角梯形ABCD中,$AC=\sqrt{2}a,AB=\sqrt{2}a,BC=2a$,
所以BC2=AC2+AB2,所以AB⊥AC,…(1分)
又因为VA⊥平面,AB?平面ABCD,所以AB⊥AV,…(2分)
而AV∩AC=A,所以AB⊥平面VAC,…(3分)
又CE?平面VAC,所以AB⊥CE.…(4分)
解:(2)取BC中点F,以点A为坐标原点,AF,AD,AV所在的直线为x,y,z轴,建立空间直角坐标系A-xyz,
不妨设AE=λAV(0<λ<1),
可得B(a,-a,0),D(0,a,0),E(0,0,λa),
故$\overrightarrow{AB}=(a,-a,0),\overrightarrow{AE}=(0,0,λa)$,…(5分)
设$\overrightarrow{m}$=(x,y,z)为平面ABE的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{AB}•\overrightarrow{m}=ax-ay=0}\\{\overrightarrow{AE}•\overrightarrow{m}=λaz=0}\end{array}\right.$,令x=1得,$\overrightarrow{m}$=(1,1,0),…(6分)
又$\overrightarrow{DE}=(0,-a,λa),\overrightarrow{DB}=(a,-2a,0)$,
设$\overrightarrow{n}$=(x,y,z)为平面DBE的一个法向量,
则$\left\{{\begin{array}{l}{-y+λz=0}\\{x-2y=0}\end{array}}\right.$,令z=1,可得$\overrightarrow{n}$=(2λ,λ,1),…(7分)
故cos<$\overrightarrow{n},\overrightarrow{m}$>=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{3λ}{\sqrt{2}•\sqrt{5{λ}^{2}+1}}$,即$cosα=\frac{3λ}{{\sqrt{2}\sqrt{5{λ^2}+1}}}$…(8分)
因为AC为VC在平面ABCD内的射影,所以∠CAV=β,
在Rt△VAC中,$tanβ=\frac{AV}{AC}=\frac{a}{{\sqrt{2}a}}=\frac{{\sqrt{2}}}{2}$,…(9分)
所以$tanαtanβ=\frac{{\sqrt{2}}}{2}$,所以tanα=1,$cosα=\frac{{\sqrt{2}}}{2}$,…(10分)
即$\frac{3λ}{{\sqrt{2}\sqrt{5{λ^2}+1}}}=\frac{{\sqrt{2}}}{2}$,解得$λ=\frac{1}{2}$或$-\frac{1}{2}$,…(11分)
又0<λ<1,所以$λ=\frac{1}{2}$,点E为VA的中点.…(12分)
点评 本题考查线线垂直的证明,考查满足条件的点的位置的确定,是中档题,解题时要认真审题,注意向量法的合理运用.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案| A. | ?x0∈R,x02-x0+1≥0 | B. | ?x0∉R,x02-x0+1≥0 | ||
| C. | ?x∈R,x2-x+1≥0 | D. | ?x∉R,x2-x+1≥0 |
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ac2<bc2 | C. | a2<b2 | D. | a3<b3 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
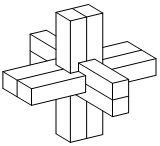 鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)
鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)