题目内容
17．如图，圆台OO1的上底面半径为6cm，下底面半径为12cm，高为3$\sqrt{5}$cm．A、B在下底面圆周上，∠AOB=135°，M是母线B1B上一点，且BM：MB1=2：1，求圆台侧面上A、M两点间的最短距离．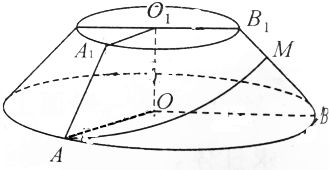
分析 由题意需先画出圆台的侧面展开图，并还原成圆锥展开的扇形，则所求的最短距离是平面图形两点连线，根据条件求出扇形的圆心角以及半径长，即可求出最短的距离．
解答 
解：由题意，画出圆台的侧面展开图，并还原成圆锥展开的扇形，
圆台所在圆锥的半径为2$\sqrt{36+45}$=18，弧AB的长为9π，
∴圆心角为$\frac{π}{2}$，
∵BM：MB1=2：1，
∴O′M=9+3=12，
∴AM=$\sqrt{1{2}^{2}+1{8}^{2}}$=6$\sqrt{13}$．
点评 本题考查了在几何体表面的最短距离的求出，一般方法是把几何体的侧面展开后，根据题意作出最短距离即两点连线，结合条件求出，考查了转化思想．
练习册系列答案
相关题目
5．有一个几何体的三视图及其尺寸如图单位（cm），则该几何体的表面积及体积为（ ）
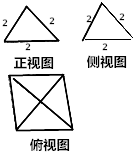
| A． | 4+4$\sqrt{3}$cm2，$\frac{16\sqrt{3}}{3}$cm3 | B． | 4+4$\sqrt{3}$cm2，$\frac{16\sqrt{2}}{3}$cm3 | C． | 12cm2，$\frac{16\sqrt{3}}{3}$cm3 | D． | 12cm2，$\frac{16\sqrt{2}}{3}$cm3 |
8．把下面在平面内成立的结论类比地推广到空间，结论还正确的是（ ）
| A． | 如果一条直线与两条平行线中的一条相交，则必与另一条相交 | |
| B． | 如果两条直线同时与第三条直线垂直，则这两条直线平行 | |
| C． | 如果两条直线同时与第三条直线相交，则这两条直线相交 | |
| D． | 如果一条直线与两条平行线中的一条垂直，则必与另一条垂直 |