题目内容
12.计算:$\underset{lim}{x→0}$$\frac{tanx-sinx}{{x}^{3}}$.分析 由$\frac{tanx-sinx}{{x}^{3}}$=$\frac{tanx(1-cosx)}{{x}^{3}}$,根据等价无穷小代换,tanx~x,1-cosx~$\frac{1}{2}{x}^{2}$,代入即可求得$\underset{lim}{x→0}$$\frac{tanx-sinx}{{x}^{3}}$的值.
解答 解:$\underset{lim}{x→0}$$\frac{tanx-sinx}{{x}^{3}}$,
=$\underset{lim}{x→0}$$\frac{tanx(1-cosx)}{{x}^{3}}$,
=$\underset{lim}{x→0}$$\frac{x•\frac{1}{2}{x}^{2}}{{x}^{3}}$,
=$\frac{1}{2}$.
点评 本题考查函数的极限,考查极限的运算,等价无穷小代换,属于基础题.

练习册系列答案
相关题目
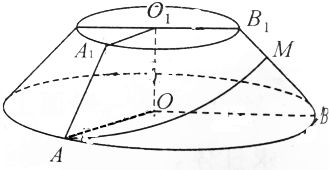
 如图所示,一个圆柱形乒乓球筒,高为40厘米,底面半径为4厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.
如图所示,一个圆柱形乒乓球筒,高为40厘米,底面半径为4厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.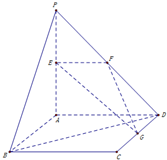 如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.