题目内容
9.已知f(x)=$\frac{2x}{x+1}$,则f($\frac{1}{2016}}$)+f(${\frac{1}{2015}}$)+…f(${\frac{1}{2}}$)+f(1)+f(2)+…+f(2016)=4031.分析 求出f(x)+f($\frac{1}{x}$)=2,从而求出答案.
解答 解:f(x)=$\frac{2x}{x+1}$,f($\frac{1}{x}$)=$\frac{\frac{2}{x}}{\frac{1}{x}+1}$=$\frac{2}{x+1}$,
∴f(x)+f($\frac{1}{x}$)=2,
∴f($\frac{1}{2016}}$)+f(${\frac{1}{2015}}$)+…f(${\frac{1}{2}}$)+f(1)+f(2)+…+f(2016)
=[f($\frac{1}{2016}$)+f(2016)]+[f($\frac{1}{2015}$)+f(2015)]+…+[f($\frac{1}{2}$)+f(2)]+f(1)
=2×2015+1=4031,
故答案为:4031.
点评 本题考查了函数求值问题,得到f(x)+f($\frac{1}{x}$)=2是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
1.对具有线性相关关系的变量x、y,有一组观测数据(xi,yi)(i=1,2,…,9),其回归方程为y=$\frac{1}{10}$x+a,且x1+x2+…+x9=10,y1+y2+…+y9=19,则实数a的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
18.关于x的不等式x2-ax+a>0恒成立,则实数a的取值范围为( )
| A. | (-∞,0)∪(2,+∞) | B. | (0,2) | C. | (-∞,0)∪(4,+∞) | D. | (0,4) |
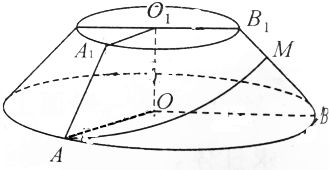

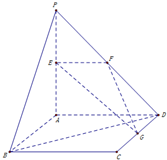 如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.