题目内容
14.已知等差数列{an}的前n项和为Sn,且a1=-20,若Sn的最小值仅为S6,则公差d的取值范围是$(\frac{10}{3},4)$.分析 利用等差数列的求和公式、二次函数的单调性即可得出.
解答 解:Sn=-20n+$\frac{n(n-1)}{2}$d=$\frac{d}{2}{n}^{2}$-$(20+\frac{d}{2})$n,
∵Sn的最小值仅为S6,则$\frac{d}{2}$>0,$5.5<\frac{20+\frac{d}{2}}{d}$<6.5,解得:$\frac{10}{3}<d<4$.
∴公差d的取值范围是$(\frac{10}{3},4)$.
故答案为:$(\frac{10}{3},4)$.
点评 本题考查了等差数列的求和公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,右焦点为F(c,0),弦PQ过F且垂直于x轴,过点P、点Q分别作直线AQ、AP的垂线,两垂线交于点B,若B到直线PQ的距离小于2(a+c),则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
2.某商场对A 商品近30 天的日销售量y(件)与时间t(天)的销售情况进行整理,得到如下数据经统计分析,日销售量y(件)与时间t(天)之间具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法原理求出 y 关于t的线性回归方程$\widehaty=bx+a$;
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
(2)已知A 商品近30 天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{t+20,(0<20,t∈N)}\\{-t+100,(20≤t≤30,t∈N)}\end{array}\right.$根据(1)中求出的线性回归方程,预测t为何值时,A 商品的日销售额最大.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}-\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$)
9.若a∈R,复数z=(a2-2a)+(a2-a-2)i是纯虚数,则( )
| A. | a≠2且a≠-1 | B. | a=0 | C. | a=2 | D. | a=0或a=2 |
4.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$\sqrt{3}$,AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,则此球的体积等于( )
| A. | $\frac{{8\sqrt{2}π}}{3}$ | B. | $\frac{9π}{2}$ | C. | $\frac{{5\sqrt{10}π}}{3}$ | D. | $\frac{{4\sqrt{3}π}}{3}$ |
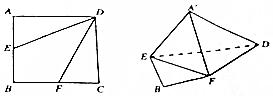 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.