题目内容
16.为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$(n=a+b+c+d)
独立性检验临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据分层抽样比计算出全班喜欢体育运动的人数和不喜欢体育运动的人数,可将列联表补充完整;
(2)根据公式计算K2,对照临界值表作结论.
解答 解:(1)设喜好体育运动的人数为x人,由已知得解得 x=30,…(2分)
列联表补充如下:
| 喜好体育运动 | 不喜好体育运动 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)∵K2=$\frac{50(20×15-10×5)^{2}}{30×20×25×25}$≈8.333>6.635…(10分)
∴可以在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关…(12分)
点评 本题考查分层抽样的统计原理,独立性检验的运用,考查学生分析解决问题的能力,是基础题.

练习册系列答案
相关题目
6.《九章算术》是我国古代的优秀数学著作,在人类历史上第一次提出负数的概念,内容涉及方程、几何、数列、面积、体积的计算等多方面.书的第6卷19题,“今有竹九节,下三节容量四升,上四节容量三升.”如果竹由下往上均匀变细(各节容量可视为等差数列),则中间剩下的两节容量是多少升( )
| A. | $2\frac{23}{66}$ | B. | $2\frac{3}{22}$ | C. | $2\frac{61}{66}$ | D. | $1\frac{10}{11}$ |
1.函数f(x)=sinωx(?>0)的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,并且函数g(x)在区间[$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3},\frac{π}{2}$]上单调递减,则实数ω的值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
8.不等式2x2-x-3>0解集为( )
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
5.设双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,右焦点为F(c,0),弦PQ过F且垂直于x轴,过点P、点Q分别作直线AQ、AP的垂线,两垂线交于点B,若B到直线PQ的距离小于2(a+c),则该双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
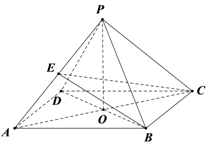 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O