题目内容

15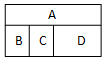．现有5种不同的颜色要对图形中（如图）的四个部分着色；要求有公共边的两部分不能用同一颜色，则不同的着色方法有180种．

分析 根据题意，从A部分开始，分4步依次分析4个部分可选颜色的情况数目，由分步计数原理计算可得答案．

解答 解：根据题意，分4步进行分析：
①、对于A部分，有5种颜色可选，即有5种情况；
②、对于B部分，与A部分有公共边，有4种颜色可选，即有4种情况；
③、对于C部分，与A、B部分都有公共边，有3种颜色可选，即有3种情况；
④、对于D部分，与A、C部分都有公共边，有3种颜色可选，即有3种情况；
则不同的着色方法有5×4×3×3=180种；
故答案为：180．

点评 本题考查排列、组合的综合应用，注意分析图形中的由公共边的部分之间的关系．

练习册系列答案
相关题目
5．对任意两实数a、b，定义运算“max{a，b}”如下：max{a，b}=$\left\{\begin{array}{l}{a（a≥b）}\\{b（a＜b）}\end{array}\right.$，则关于函数f（x）=max{sinx，cosx}，下列命题中：
①函数f（x）的值域为[-$\frac{\sqrt{2}}{2}$，1]；         
②函数f（x）是周期函数；
③函数f（x）的对称轴为x=kπ+$\frac{π}{4}（k∈{Z}）$；
④当且仅当x=2kπ（k∈Z）时，函数f（x）取得最大值1；
⑤当且仅当2kπ＜x＜2kπ+$\frac{3}{2}π（k∈{Z}）$时，f（x）＜0；
正确的是①②③（填上你认为正确的所有答案）
6．（Ⅰ）已知$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{5}{7}$，求sinα•cosα的值；
（Ⅱ）求$\frac{{\sqrt{1-2sin{{10}°}cos{{10}°}}}}{{cos{{10}°}-\sqrt{1-{{cos}^2}{{170}°}}}}$的值．
3．在△ABC中，内角A，B，C的对边分别为a，b，c，若$a=3，b=\sqrt{6}，∠A=\frac{2π}{3}$，则∠B=（　　）
A．$\frac{π}{4}$或$\frac{π}{6}$B．$\frac{π}{12}$C．$\frac{π}{4}$D．$\frac{π}{6}$
10．已知$a=sin\frac{2π}{7}$，$b=cos\frac{12π}{7}$，$c=tan\frac{9π}{7}$，则（　　）
A．a＞b＞cB．c＞b＞aC．c＞a＞bD．a＞c＞b
20．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点M（2，0），N（0，1）两点．
（1）求椭圆C的方程及离心率；
（2）直线y=kx（k∈R，k≠0）与椭圆C相交于A，B两点，D点为椭圆C上的动点，且|AD|=|BD|，请问△ABD的面积是否存在最小值？若存在，求出此时直线AB的方程：若不存在，说明理由．
7．已知函数f（x）=f?（$\frac{π}{4}$）cosx+sinx，则f（$\frac{3π}{4}$）=（　　）
A．$\sqrt{2}$B．$\sqrt{2}$-1C．1D．0
4．已知向量$\overrightarrow a，\overrightarrow b$满足：$|{\overrightarrow a}|=2，|{\overrightarrow b}|=4$，且$（\overrightarrow a-\overrightarrow b）•\overrightarrow b=-20$．
（1）求证：$（\overrightarrow a+\overrightarrow b）⊥\overrightarrow a$；
（2）求向量$\overrightarrow a$与$\overrightarrow b$的夹角．
5．等差数列{an}满足an＞0，$a_4^2+a_7^2+2{a_4}{a_7}=9$，则其前10项之和为（　　）
A．-9B．15C．-15D．±15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网