题目内容
4.已知向量$\overrightarrow a,\overrightarrow b$满足:$|{\overrightarrow a}|=2,|{\overrightarrow b}|=4$,且$(\overrightarrow a-\overrightarrow b)•\overrightarrow b=-20$.(1)求证:$(\overrightarrow a+\overrightarrow b)⊥\overrightarrow a$;
(2)求向量$\overrightarrow a$与$\overrightarrow b$的夹角.
分析 (1)先计算$\overrightarrow{a}•\overrightarrow{b}$,再计算($\overrightarrow{a}+\overrightarrow{b}$)$•\overrightarrow{a}$=0即可得出结论;
(2)代入夹角公式计算即可.
解答 证明:(1)∵$|{\overrightarrow b}|=4,(\overrightarrow a-\overrightarrow b)•\overrightarrow b=-20$,∴$\overrightarrow a•\overrightarrow b-{\overrightarrow b^2}=\overrightarrow a•\overrightarrow b-16=-20$,
∴$\overrightarrow a•\overrightarrow b=-4$,
∵$|{\overrightarrow a}|=2$,
∴$(\overrightarrow a+\overrightarrow b)•\overrightarrow a={\overrightarrow a^2}+\overrightarrow a•\overrightarrow b=0$,
∴$(\overrightarrow a+\overrightarrow b)⊥\overrightarrow a$.
(2)设向量$\overrightarrow a$与$\overrightarrow b$的夹角为θ,则$cosθ=\frac{\overrightarrow a,\overrightarrow b}{{|{\overrightarrow a}|•|{\overrightarrow b}|}}=-\frac{1}{2}$,
θ=1200.即向量$\overrightarrow a$与$\overrightarrow b$的夹角为120°.
点评 本题考查了平面向量的数量积运算,属于中档题.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | $\sqrt{5}$ | B. | $-\sqrt{5}$ | C. | 2 | D. | -2 |
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}}\\{\hat a=\bar y-\hat b\bar x}\end{array}}\right.$.
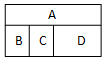 现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.
现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.