题目内容
3.在△ABC中,内角A,B,C的对边分别为a,b,c,若$a=3,b=\sqrt{6},∠A=\frac{2π}{3}$,则∠B=( )| A. | $\frac{π}{4}$或$\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 由已知及正弦定理可得:sinB=$\frac{\sqrt{2}}{2}$,由大边对大角可得B为锐角,即可得解B=$\frac{π}{4}$.
解答 解:∵$a=3,b=\sqrt{6},∠A=\frac{2π}{3}$,
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{6}×\frac{\sqrt{3}}{2}}{3}$=$\frac{\sqrt{2}}{2}$,
∵b<a,B为锐角,
∴B=$\frac{π}{4}$.
故选:C.
点评 本题主要考查了正弦定理,大边对大角在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
13.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),(点P与点A,B不重合),则△PAB的面积最大值是( )
| A. | $2\sqrt{5}$ | B. | 5 | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$ |
8.下表数据为某地区某基地某种农产品的年产量x(单位:吨)及对应销售价格y(单位:万元/吨).
(1)若y与x有较强的线性相关关系,请用最小二乘法求出y关与x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)若每吨该农产品的成本为1万元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润z最大?最大利润是多少?
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{({{x_i}{y_i}})}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 1 | 2 | 3 |
| y | 5 | 4 | 3 |
(2)若每吨该农产品的成本为1万元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润z最大?最大利润是多少?
参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{({{x_i}{y_i}})}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
12.若角α的终边经过点(α,-1),且$tanα=-\frac{1}{2}$,则α=( )
| A. | $\sqrt{5}$ | B. | $-\sqrt{5}$ | C. | 2 | D. | -2 |
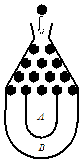 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.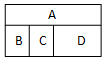 现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.
现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.