题目内容
5.对任意两实数a、b,定义运算“max{a,b}”如下:max{a,b}=$\left\{\begin{array}{l}{a(a≥b)}\\{b(a<b)}\end{array}\right.$,则关于函数f(x)=max{sinx,cosx},下列命题中:①函数f(x)的值域为[-$\frac{\sqrt{2}}{2}$,1];
②函数f(x)是周期函数;
③函数f(x)的对称轴为x=kπ+$\frac{π}{4}(k∈{Z})$;
④当且仅当x=2kπ(k∈Z)时,函数f(x)取得最大值1;
⑤当且仅当2kπ<x<2kπ+$\frac{3}{2}π(k∈{Z})$时,f(x)<0;
正确的是①②③(填上你认为正确的所有答案)
分析 画出函数y=f(x)的图象,通过函数图象可以直观的看出何时取到最值,对称轴以及周期性等问题.
解答 解:画出函数y=f(x)的图象如图所示;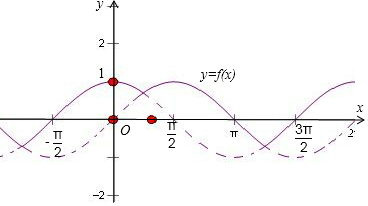
由图可知:
①函数f(x)的值域为[-$\frac{\sqrt{2}}{2}$,1],∴①正确;
②函数f(x)是最小正周期为2π的函数,∴②正确;
③函数f(x)的对称轴为x=kπ+$\frac{π}{4}(k∈{Z})$,∴③正确;
④x=2kπ或x=2kπ+$\frac{π}{2}$(k∈Z)时,函数f(x)取得最大值1,∴④错误;
⑤当且仅当2kπ+π<x<2kπ+$\frac{3}{2}π(k∈{Z})$时,f(x)<0,∴⑤错误;
综上,正确的命题序号是①②③.
故答案为:①②③.
点评 本题考查了分段函数的定义、图象与性质的应用问题,也考查了画图与识图的能力,是中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
15.若f(x)在x0处可导,则$lim\frac{{f({x_0}-△x)-f({x_0})}}{△x}$=( )
| A. | f(x0) | B. | -f′(x0) | C. | f′(-x0) | D. | 不一定存在 |
13.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),(点P与点A,B不重合),则△PAB的面积最大值是( )
| A. | $2\sqrt{5}$ | B. | 5 | C. | $\frac{5}{2}$ | D. | $\sqrt{5}$ |
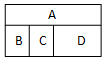 现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.
现有5种不同的颜色要对图形中(如图)的四个部分着色;要求有公共边的两部分不能用同一颜色,则不同的着色方法有180种.