题目内容
如果ax2+ax+1≥0恒成立,求a的取值范围.
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用
分析:通过讨论a的范围,结合二次函数的性质从而求出a的范围.
解答:
解:①当a=0,不等式ax2+ax+1>0变为1>0,对任意实数x恒成立;
②当a≠0时,对任意实数x都有ax2+ax+1>0恒成立,需
,解得0<a<4,
综上:a∈{a|0≤a<4].
②当a≠0时,对任意实数x都有ax2+ax+1>0恒成立,需
|
综上:a∈{a|0≤a<4].
点评:本题考查了二次函数的性质,考查了分类讨论思想,是一道基础题.

练习册系列答案
相关题目
从1,2,3,4,5这5个数中任取两数,其中:①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数. 上述事件中,是对立事件的是( )
| A、① | B、②④ | C、③ | D、①③ |
已知某几何体的三视图如图所示,则该几何体的体积为( )
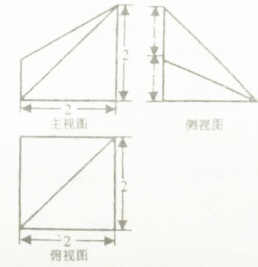

A、
| ||||
| B、8 | ||||
C、
| ||||
D、
|
若函数f(x)=
+
,其中x∈[-
,a],若f(x)的值域是[-
,1],则a的取值范围是( )
| ||
| 2 |
| cos2x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
若复数
(i为虚数単位)是纯虚数,则实数 a的值为( )
| 1+ai |
| 2+i |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
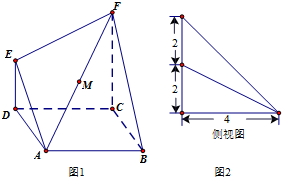 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=