题目内容
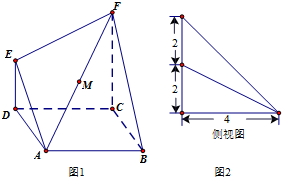 在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=
在如图1所示的多面体ABCDEF中,四边形ABCD是正方形,ED⊥平面ABCD,ED∥FC,ED=| 1 |
| 2 |
(Ⅰ)求证:EM∥平面ABCD;
(Ⅱ)求证:平面AEF⊥平面FAC;
(Ⅲ)若图2是该多面体的侧视图,求四棱锥A-CDEF的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)连接AC,BD,设AC∩BD=O,连接OM,证明EM∥DO,利用直线与平面平行的判定定理证明EM∥平面ABCD.
(Ⅱ)证明CF⊥底面ABCD,DO⊥平面FAC.然后证明EM⊥平面FAC.利用平面与平面垂直的判定定理证明平面AEF⊥平面FAC.
(Ⅱ)说明AD⊥平面EDCF.得到棱锥的高,然后代入体积公式求解即可.
(Ⅱ)证明CF⊥底面ABCD,DO⊥平面FAC.然后证明EM⊥平面FAC.利用平面与平面垂直的判定定理证明平面AEF⊥平面FAC.
(Ⅱ)说明AD⊥平面EDCF.得到棱锥的高,然后代入体积公式求解即可.
解答:
满分(12分).
解:(Ⅰ)连接AC,BD,设AC∩BD=O,则O为BD的中点.
连接OM,则MO∥FC,且MO=
FC.…1′分
又∵ED∥FC,且ED=
FC,∴MO∥ED,且MO=ED,
∴EDOM是平行四边形,EM∥DO.…(2分)
∵EM?平面ABCD,DO?平面ABCD,
∴EM∥平面ABCD. …(4分)
(Ⅱ)∵ED∥FC,ED⊥底面ABCD,
∴CF⊥底面ABCD,…(5分)
又∵DO?平面ABCD,∴CF⊥DO.
∵四边形ABCD是正方形,∴AC⊥DO.
∵CF,AC?平面FAC,CF∩AC=C,
∴DO⊥平面FAC.…(7分)
由(Ⅰ)知EM∥DO,
∴EM⊥平面FAC. …(8分)
又∵EM?平面AEF,∴平面AEF⊥平面FAC. …(9分)
(Ⅱ)由侧视图可知,ED=2,DC=CF=4.…(10分)
∵四边形ABCD是正方形,∴AD=4.
∵ED⊥平面ABCD,AD?面ABCD,∴ED⊥AD,
又∵AD⊥DC,ED∩DC=D,∴AD⊥平面EDCF. …(11分)
则VA-EDCF=
•AD•SEDCF=
×4×
=16.…(12分)
解:(Ⅰ)连接AC,BD,设AC∩BD=O,则O为BD的中点.
连接OM,则MO∥FC,且MO=
| 1 |
| 2 |
又∵ED∥FC,且ED=
| 1 |
| 2 |
∴EDOM是平行四边形,EM∥DO.…(2分)
∵EM?平面ABCD,DO?平面ABCD,
∴EM∥平面ABCD. …(4分)
(Ⅱ)∵ED∥FC,ED⊥底面ABCD,
∴CF⊥底面ABCD,…(5分)
又∵DO?平面ABCD,∴CF⊥DO.
∵四边形ABCD是正方形,∴AC⊥DO.
∵CF,AC?平面FAC,CF∩AC=C,
∴DO⊥平面FAC.…(7分)
由(Ⅰ)知EM∥DO,
∴EM⊥平面FAC. …(8分)
又∵EM?平面AEF,∴平面AEF⊥平面FAC. …(9分)
(Ⅱ)由侧视图可知,ED=2,DC=CF=4.…(10分)
∵四边形ABCD是正方形,∴AD=4.
∵ED⊥平面ABCD,AD?面ABCD,∴ED⊥AD,
又∵AD⊥DC,ED∩DC=D,∴AD⊥平面EDCF. …(11分)
则VA-EDCF=
| 1 |
| 3 |
| 1 |
| 3 |
| (2+4)×4 |
| 2 |
点评:本小题主要考查空间中直线与平面的位置关系、几何体体积等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想等.

练习册系列答案
相关题目
对于函数y=sin(2x-
),下列说法正确的是( )
| π |
| 6 |
A、函数图象关于点(
| ||||
B、函数图象关于直线x=
| ||||
C、将它的图象向左平移
| ||||
D、将它的图象上各点的横坐标缩小为原来的
|