Question

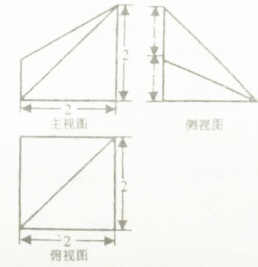
已知某几何体的三视图如图所示，则该几何体的体积为（　　）

• A、

  8

  3

• B、8
• C、

  10

  3

• D、

  1

  3

  +

  2

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知中的三视图可得该几何体的直观图，进而将其分割成一个四棱锥和一个三棱锥，分别求出体积，相加可得答案．

解答： 解：由已知中的三视图可得该几何体的直观图如下所示：

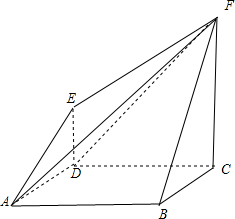
连接FD，则该几何体可分成四棱锥F-ABCD和三棱锥F-ADE，
四棱锥F-ABCD的底面是边长为2的正方形，高为2，故体积V=

1

3

×2×2×2=

8

3

，
三棱锥F-ADE，底面为两直角边为1和2的三角形，高为2，故体积V=

1

3

×

1

2

×2×1×2=

2

3

，
故该几何体的体积为

10

3

，
故选：C

点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．