题目内容
19.已知$sinθ-cosθ=-\frac{1}{5}$(1)求sinθcosθ的值.
(2)求sin3θ-cos3θ的值.
(3)当-π<θ<0时,求tanθ的值.
分析 (1)将已知等式两边平方,利用同角三角函数基本关系式即可得解.
(2)利用同角三角函数基本关系式及立方差公式即可得解.
(3)把已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,求出sinθ+cosθ的值,与已知等式联立求出sinθ与cosθ的值,即可确定出tanθ的值.
解答 解:(1)∵$sinθ-cosθ=-\frac{1}{5}$,
∴两边平方可得:1-2sinθcosθ=$\frac{1}{25}$,解得:sinθcosθ=$\frac{12}{25}$.
(2)sin3θ-cos3θ=(sinθ-cosθ)(sin2θ+sinθcosθ+cos2θ)=(-$\frac{1}{5}$)×(1+$\frac{12}{25}$)=-$\frac{37}{125}$.
(3)∵sinθcosθ=$\frac{12}{25}$,$sinθ-cosθ=-\frac{1}{5}$①.
∴由-π<θ<0,可得:-π<θ<$-\frac{π}{2}$,
∵(sinθ+cosθ)2=1+2sinθcosθ=$\frac{49}{25}$,
∴sinθ+cosθ=-$\frac{7}{5}$②,
联立①②,解得:sinθ=-$\frac{4}{5}$,cosθ=-$\frac{3}{5}$,
则tanθ=$\frac{sinθ}{cosθ}$=$\frac{4}{3}$.
点评 此题考查了同角三角函数基本关系的运用,考查了计算能力和转化思想,熟练掌握基本关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.函数y=cos2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后,与函数y=sin(2x-$\frac{π}{6}$)的图象重合,则φ=( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
7.复数$\frac{i}{1-2i}$(i为虚数单位)的共轭复数为( )
| A. | $\frac{-2+i}{5}$ | B. | $\frac{-2-i}{5}$ | C. | $\frac{2-i}{5}$ | D. | $\frac{2+i}{5}$ |
14.有一段演绎推理是这样的:“若对数函数y=logax是增函数,已知y=${log_{\frac{1}{4}}}x$是对数函数,则y=${log_{\frac{1}{4}}}x$是增函数”
以上推理的错误是( )
以上推理的错误是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和小前提错误导致结论错误 |
4.当m=7时,执行如图所示的程序框图,输出的S值为( )
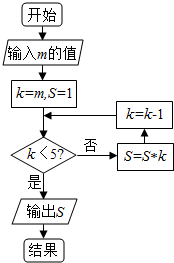

| A. | 7 | B. | 42 | C. | 210 | D. | 840 |
8.已知集合U=R,A={y|y=x2+x},B={y|y=($\frac{1}{2}$)x},则∁UB)∩A=( )
| A. | [-$\frac{1}{4}$,0] | B. | (0,$\frac{1}{4}$] | C. | (-∞,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,1) |
