题目内容
过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于A，B两点，交准线于点C若
=2
，则直线AB的斜率为 ．
| CB |
| BF |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先求当C点在B点的下方时，由B向准线作垂线，垂足为B•，根据抛物线定义可知|BB′|=|BF|，根据
=2
，判断2|BB′|=|CB|进而可知∠C=30°，∠CBO=60°，可得直线AB的斜率，同理可求得当C点在A点上方时直线的斜率．
| CB |
| BF |
解答：
解：当C点在B点的下方时，
由B向准线作垂线，垂足为B•，根据抛物线定义可知|BB′|=|BF|，
∵
=2
，∴2|BB′|=|CB|
∴∠C=30°
∴∠CBO=60°
∴直线AB的斜率为tan∠CBO=
同理可求得当C点在A点上方时tan∠CBO=-
．
故答案为：±
．
由B向准线作垂线，垂足为B•，根据抛物线定义可知|BB′|=|BF|，
∵
| CB |
| BF |
∴∠C=30°
∴∠CBO=60°
∴直线AB的斜率为tan∠CBO=
| 3 |
同理可求得当C点在A点上方时tan∠CBO=-
| 3 |
故答案为：±
| 3 |
点评：本题主要考查抛物线的应用．涉及抛物线的焦点弦的时候，常用应用抛物线的定义．注意本题有两解．
练习册系列答案
相关题目
为了有效管理学生迟到问题，某校专对各班迟到现象制定了相应的等级标准，其中D级标准为“连续10天，每天迟到不超过7人”根据过去10天1、2、3、4班的迟到数据，一定符合D级标准的是（ ）
| A、1班：总体平均值为3，中位数为4 |
| B、2班：总体平均值为1，总体方差大于0 |
| C、3班：中位数为2，众数为3 |
| D、4班：总体平均值为2，总体方差为3 |
设函数f（x）=
，g（x）=
，则函数f（x）•g（x）的定义域是（ ）
| 3 | 3x-2 |
| 1 | ||
|
A、[
| ||||
B、（
| ||||
C、[
| ||||
D、（
|
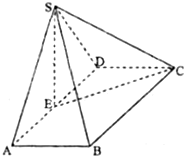如图，在四棱锥S-ABCD中，底面ABCD为矩形，侧面SAD为边长2的正三角形，且面SAD⊥面ABCD．AB=