题目内容
新城建设中某项工程,由甲、乙两工程队合作10天可完成.已知甲工程队单独施工比乙工程队单独施工多用15天完成此项工程.甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)这项工程由甲工程队单独施工a天后,再由甲、乙两工程队合作施工完成剩下的工程.如果总工期不能超过24天,并且施工费不超过32万元,求a的取值范围.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)这项工程由甲工程队单独施工a天后,再由甲、乙两工程队合作施工完成剩下的工程.如果总工期不能超过24天,并且施工费不超过32万元,求a的取值范围.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)利用甲10天的工作量+乙10天的工作量=1,列方程求出即可即可;
(2)关系式为:总工期不能超过24天,甲需要的工程费+乙需要的工程费≤32,进而求解.
(2)关系式为:总工期不能超过24天,甲需要的工程费+乙需要的工程费≤32,进而求解.
解答:
解:(1)设乙单独完成此项工程需要x天,则甲单独完成此项工程需要(x+15)天.
根据题意得出:10(
+
)=1,
解得:x=15,
经检验x=15是原方程的解,合题意,.
∴x+15=30;
(2)根据题意得出:
a+
×(1+2.5)≤32,且a+
≤24
解得:18≤a≤36.
根据题意得出:10(
| 1 |
| x |
| 1 |
| x+15 |
解得:x=15,
经检验x=15是原方程的解,合题意,.
∴x+15=30;
(2)根据题意得出:
a+
1-
| ||
|
1-
| ||
|
解得:18≤a≤36.
点评:此题主要考查了分式方程与一元一次不等式的应用,关键是首先弄清题意,找出题目中的等量关系或不等关系,列出方程或不等式,此题用到的公式是:工作效率×工作时间=工作量.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、根据通项公式可以求出数列的任何一项 |
| B、任何数列都有通项公式 |
| C、一个数列可能有几个不同形式的通项公式 |
| D、有些数列可能不存在最大项 |
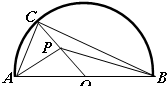 如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(
如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(| PA |
| PB |
| PC |
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |