题目内容
设双曲线C经过点(2,2),且与
-x2=1具有相同渐进线,则双曲线C的方程为 .
| y2 |
| 4 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线渐近线之间的关系,利用待定系数法即可得到结论.
解答:
解:与
-x2=1具有相同渐近线的双曲线方程可设为
-x2=m,(m≠0),
∵双曲线C经过点(2,2),
∴m=-3,
即双曲线方程为
-x2=-3,即
-
=1
故答案为:
-
=1.
| y2 |
| 4 |
| y2 |
| 4 |
∵双曲线C经过点(2,2),
∴m=-3,
即双曲线方程为
| y2 |
| 4 |
| x2 |
| 3 |
| y2 |
| 12 |
故答案为:
| x2 |
| 3 |
| y2 |
| 12 |
点评:本题主要考查双曲线的性质,利用渐近线之间的关系,利用待定系数法是解决本题的关键,比较基础.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
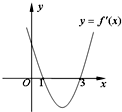 已知函数f(x)=x3+ax2+bx+c的导函数y=f′(x)的图象如图所示,给出下列三个结论:
已知函数f(x)=x3+ax2+bx+c的导函数y=f′(x)的图象如图所示,给出下列三个结论:①f(x)的单调递减区间是(1,3);
②函数f(x)在x=1处取得极小值;
③a=-6,b=9.正确的结论是( )
| A、①③ | B、①② | C、②③ | D、①②③ |
已知
,
为不共共线的非零向量,且|
|=|
|=1,则以下四个向量中模最大者为( )
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,且AB∥CD,BC⊥AB,BC=CD=BO=PO,EA=AO=
如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,且AB∥CD,BC⊥AB,BC=CD=BO=PO,EA=AO=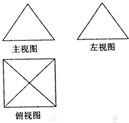 一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )
一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )