题目内容
19.在平面直角坐标系xOy中,圆C1:(x+1)2+(y-6)2=25,圆C2:(x-17)2+(y-30)2=r2,若圆C2上存在一点P,使得过点P可作一条射线与圆C1一次交于点A,B,满足|PA|=2|AB|,则半径r的取值范围是( )| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
分析 求出两个圆的圆心距,画出示意图,利用已知条件判断半径r的取值范围即可.
解答 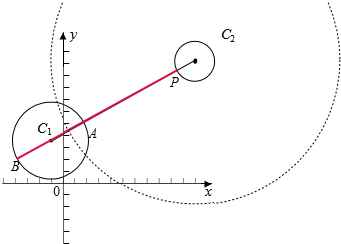 解:圆C1:(x+1)2+(y-6)2=25,圆心(-1,6);半径为:5.
解:圆C1:(x+1)2+(y-6)2=25,圆心(-1,6);半径为:5.
圆C2:(x-17)2+(y-30)2=r2.圆心(17,30);半径为:r.
两圆圆心距为:$\sqrt{(17+1)^{2}+(30-6)^{2}}$=30.
如图:PA=2AB,可得AB的最大值为直径,
此时C2A=20,r>0.当半径扩大到55时,此时圆C2上只有一点到C1的距离为25,而且是最小值,半径再大,没有点满足PA=2AB.
∴r∈[5,55].
故选:A.
点评 本题考查两个圆的位置关系.直线与圆的综合应用.考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.直线l1:2x-y-1=0与直线l2:mx+4y+2=0互相平行的充要条件是( )
| A. | m=-8 | B. | $m=-\frac{1}{2}$ | C. | m=8 | D. | m=2 |
8.已知全集U=R,集合A={x|y=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x+1)}}$},B={x|($\frac{1}{2}$)x≤1},则∁U(A∪B)=( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | (-∞,$\frac{1}{2}$) |