题目内容
8.已知全集U=R,集合A={x|y=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x+1)}}$},B={x|($\frac{1}{2}$)x≤1},则∁U(A∪B)=( )| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | (-∞,$\frac{1}{2}$) |
分析 根据对数函数、指数函数的单调性可以解出A=$(-\frac{1}{2},0)$,B=[0,+∞),然后进行并集、补集的运算即可.
解答 解:解$lo{g}_{\frac{1}{2}}(2x+1)>0$得,$-\frac{1}{2}<x<0$;
解$(\frac{1}{2})^{x}≤1$得,x≥0;
∴$A=(-\frac{1}{2},0),B=[0,+∞)$;
∴$A∪B=(-\frac{1}{2},+∞)$;
∴${∁}_{U}(A∪B)=(-∞,-\frac{1}{2}]$.
故选:C.
点评 考查对数函数、指数函数的单调性,以及对数函数、指数函数的定义域,并集与补集的运算.

练习册系列答案
相关题目
19.在平面直角坐标系xOy中,圆C1:(x+1)2+(y-6)2=25,圆C2:(x-17)2+(y-30)2=r2,若圆C2上存在一点P,使得过点P可作一条射线与圆C1一次交于点A,B,满足|PA|=2|AB|,则半径r的取值范围是( )
| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
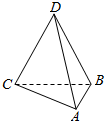 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )