题目内容
11.向量$\overrightarrow{a}$,$\overrightarrow{b}$所在的直线分别是l1,l2.(1)若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,试探讨l1与l2的关系;
(2)试探讨(1)的逆命题是否成立.
分析 (1)将条件两边平方,化简可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,可得直线l1与l2垂直;
(2)(1)的逆命题:若直线l1⊥l2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,也成立.由向量垂直的条件和完全平方公式,即可得到结论.
解答 解:(1)若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
即为($\overrightarrow{a}$+$\overrightarrow{b}$)2=($\overrightarrow{a}$-$\overrightarrow{b}$)2,
即$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2+$\overrightarrow{b}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$,
即有$\overrightarrow{a}$•$\overrightarrow{b}$=0,
则$\overrightarrow{a}$⊥$\overrightarrow{b}$,
即有直线l1与l2垂直;
(2)(1)的逆命题:若直线l1⊥l2,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,也成立.
由直线l1⊥l2,可得$\overrightarrow{a}$⊥$\overrightarrow{b}$,
即$\overrightarrow{a}$•$\overrightarrow{b}$=0,即有$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2+$\overrightarrow{b}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$,
则($\overrightarrow{a}$+$\overrightarrow{b}$)2=($\overrightarrow{a}$-$\overrightarrow{b}$)2,
即有|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|.
点评 本题考查向量的数量积的性质,考查向量垂直的条件:数量积为0,向量的平方即为模的平方.考查推理能力,属于基础题.

(2)函数$g(x)=\frac{2}{x}+lnx+x-2-b(b∈R)$.在区间[e-1,e]上有两个零点,求实数b的取值范围;
(3)完成填空
| 用方程表述 | 用函数零点表述 | |
| 若函数y=f(x)和y=g(x)的图象在(a,b)内有交点 |
| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
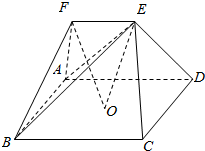 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.