题目内容
9.y=4x-2x+1的单调递减区间是(-∞,-1].分析 令 2x=t>0,可得y=${(t-\frac{1}{2})}^{2}$+$\frac{3}{4}$,可得当t∈(0,$\frac{1}{2}$],即x∈(-∞,-1]时,函数y单调递减,从而得出结论.
解答 解:令 2x=t>0,可得y=t2-t+1=${(t-\frac{1}{2})}^{2}$+$\frac{3}{4}$,
故当t∈(0,$\frac{1}{2}$],即x∈(-∞,-1]时,函数y单调递减;
故当t∈($\frac{1}{2}$,+∞),即x∈(-1,+∞)时,函数y单调递增,
故函数y的减区间为∈(-∞,-1],
故答案为:(-∞,-1].
点评 本题主要考查复合函数的单调性、指数函数、二次函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.在平面直角坐标系xOy中,圆C1:(x+1)2+(y-6)2=25,圆C2:(x-17)2+(y-30)2=r2,若圆C2上存在一点P,使得过点P可作一条射线与圆C1一次交于点A,B,满足|PA|=2|AB|,则半径r的取值范围是( )
| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
17.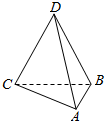 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )| A. | 4π | B. | 12π | C. | 16π | D. | 36π |
14.已知函数f(x)=x2+2x+a-1,当x∈(-∞,-3)时,f(x)>0恒成立.则实数a的取值范围是( )
| A. | a>-2 | B. | a≥-2 | C. | a>2 | D. | a≥2 |
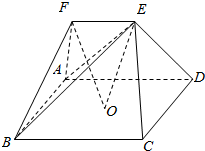 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.