题目内容
14．若某几何体的三视图（单位：cm）如图所示，则此几何体的表面积是（ ）cm2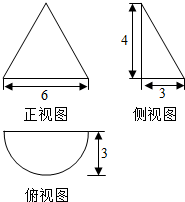
| A． | 12π | B． | 24π | C． | 15π+12 | D． | 12π+12 |
分析 由三视图得此几何体是半个圆锥：底面是以3cm为半径的圆、以5cm为母线，高为4cm，并由三视图求出相应的数据，由表面积公式求出答案．
解答 解：由三视图得，此几何体是半个圆锥：
底面是以3cm为半径的圆、以5cm为母线，高h=4cm，
所以此几何体的表面积S=$\frac{1}{2}πrl$+$\frac{1}{2}π{r}^{2}$+rh=12π+12（cm2），
故选：D．
点评 本题考查由三视图求几何体的表面积，解题关键是判断几何体的形状及几何量所对应的数据，考查空间想象能力．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
16．已知平面α内的三点A（0，0，1）、B（0，1，0）、C（1，0，0），平面β的一个法向量为（-1，-1，-1），且β与α不重合（ ）
| A． | α∥β | B． | α⊥β | ||
| C． | α与β相交但不垂直 | D． | 以上都不对 |
9．双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两个焦点为F1、F2，以线段F1F2为边作正三角形MF1F2，若MF1的中点在双曲线上，则$\frac{{b}^{2}}{{a}^{2}}$=（ ）
| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$+1 | C． | 3+2$\sqrt{3}$ | D． | 4+2$\sqrt{3}$ |
6．记$\sum_{i=1}^{n}$ai=a1+a2+…+an，$\underset{\stackrel{n}{π}}{i=1}$ai=a1×a2×…×an，设关于实数x的函数fn（x）=$\frac{nx-n}{\underset{\stackrel{n}{π}}{i=1}[ix-（i-1）]}$（n∈N*）满足$\sum_{i=1}^{2015}$fi（x）＜1，则x可取的值为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{7}{12}$ | C． | $\frac{31}{40}$ | D． | $\frac{49}{60}$ |
3．已知集合A={a，c，d}，B={b，d，e}，U=A∪B，则A∩（∁UB）为（ ）
| A． | {a，c，d，e} | B． | {a，c} | C． | {b，d} | D． | {d} |
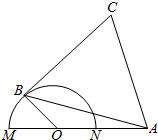如图半⊙O的直径为2，A为直径MN延长线上一点，且OA=2，B为半圆周上任一点，以AB为边作等边△ABC（A、B、C按顺时针方向排列）问∠AOB为多少时，四边形OACB的面积最大？这个最大面积是多少？