题目内容
19.设向量$\overrightarrow{a}$=(-1,1)与$\overrightarrow{b}$=(0,2),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$.分析 由已知向量的坐标求出$\overrightarrow{a}•\overrightarrow{b},|\overrightarrow{a}|,|\overrightarrow{b}|$,然后直接代入数量积求夹角公式得答案.
解答 解:∵$\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(0,2),
∴$\overrightarrow{a}•\overrightarrow{b}=2$,
$|\overrightarrow{a}|=\sqrt{2},|\overrightarrow{b}|=2$,
则cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}=\frac{2}{2\sqrt{2}}=\frac{\sqrt{2}}{2}$.
∴$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$.
故答案为:$\frac{π}{4}$
点评 本题考查平面向量的数量积运算,训练了利用数量积求向量的夹角,是基础的计算题.

练习册系列答案
相关题目
14.若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )cm2
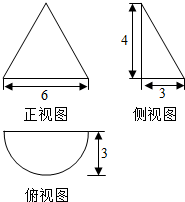

| A. | 12π | B. | 24π | C. | 15π+12 | D. | 12π+12 |
4.“点P(1,2)在曲线x2+a2y2-5=0上”是“a=1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
11.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,体积为$\frac{16}{3}$,则该球的表面积为( )
| A. | $\frac{81π}{4}$ | B. | 16π | C. | 9π | D. | $\frac{27π}{4}$ |
9.设复数z=$\frac{1}{1-i}$+i(i为虚数单位),则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | 2 |