题目内容
9.双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点为F1、F2,以线段F1F2为边作正三角形MF1F2,若MF1的中点在双曲线上,则$\frac{{b}^{2}}{{a}^{2}}$=( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | 3+2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
分析 先根据双曲线方程求得焦点坐标的表达式,进而可求得三角形的高,则点M的坐标可得,进而求得其中点N的坐标,代入双曲线方程求得a,b和c的关系式化简整理求得关于e的方程求得e.
解答 解:依题意可知双曲线的焦点为F1(-c,0),F2(c,0)
∴F1F2=2c
∴三角形高是$\sqrt{3}$c
M(0,$\sqrt{3}$c)
所以中点N(-$\frac{c}{2}$,$\frac{\sqrt{3}}{2}$c)
代入双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,整理得:b2c2-3a2c2=4a2b2
∵c2=b2+a2
所以b4-6a2b2-3a4=0,
整理得($\frac{{b}^{2}}{{a}^{2}}$)2-6×$\frac{{b}^{2}}{{a}^{2}}$-3=0.
求得$\frac{{b}^{2}}{{a}^{2}}$=$3+2\sqrt{3}$.
故选:C.
点评 本题主要考查了双曲线的简单性质.考查了学生对双曲线的基础知识的把握.分析问题解决问题的能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
14.若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )cm2
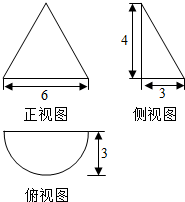

| A. | 12π | B. | 24π | C. | 15π+12 | D. | 12π+12 |
18.为了得到函数y=$\frac{1}{2}$sin4x-$\frac{\sqrt{3}}{2}$cos4x的图象,可以将函数y=sin4x的图象( )
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |